|
|
|
|
Главная >> Решенния упражнений к учебнику Макарычева. Алгебра 7 класс |
|
|
Домашние работы Дополнительные упражнения к параграфу 7 (окончание)529. х6 - х5 + х4 - х3 + х2 - х + 1 = 0 ⇒ х6 - х5 + х4 - х3 + х2 - х = -1 ⇒ х5 • (х - 1) + х3 • (х - 1) + x • (х - 1) = -1 ⇒ (х - 1) • (х5 + х3 + х) = -1 — при х < 0, значение с х - 1 отрицательное, х5 + х3 + х так же отрицательно, при перемножении двух отрицательных чисел получится положительное число, а должно -1, значит уравнение х6 - х5 + х4 - х3 + х2 - х + 1 = 0 не имеет отрицательных корней. 530. a) a10a12 (-a5) = -a10 + 12 + 5 = -a27; б) x • (-x) (-x6) = x6 + 1 + 1 = x8; в) yky8y2 = yk + 8 + 2 = yk + 10. г) bnbnb3 = bn + n + 3 = b2n+3. 531. a) 25 • 8 = 25 • 23 = 25 + 3 = 28; 6) 16 • 64 = 24 • 26 = 24 + 6 = 210; в) 7n • 343 = 7n • 73 = 7n + 3; г) 81 • 3k = 34 • 3k = 34m+ k. 532. a) a10 = a10 - 5 • a5 • a5a5; 6) a6 = a6 - 5 • a5 = a • a5; в) —a40 = -a40 - 5 • a5 = -a35 • a5. 533. a) c2x = c5 ⇒ x = c5 - 2 = c3; 6) xc5 = c9 ⇒ x = c9 - 5 = c4; в) c6x = c11 ⇒ x = c11 - 6 = c5; r) с4x = c15 ⇒x = c15 - 4 = c11. 534. a) b15 : b12 = b15 - 12 = b3; б) 739 : 713 = 739 - 13 = 726; в) a11 : a = a11 - 1 = a10; г) 12100 : 1299 = 12100 - 99 = 12.
536. a) 6n + 3 : 6n = 6n + 3 - n = 63 = 216; 6) 10n + 1 : 10n - 1 = 10n + 1 - (n - 1) = 10n + 1 - n + 1 = 102 = 100.
538. a) (-1)n • (-1)n = (-1)2n = 1 — так как показатель степени чётный; б) (-1)2n : (-1)3 = 1 : (-1) = -1. 539. S = πr2: S3 = π(3r)2 = 9πr2 — площадь увеличится в 9 раз; S7 = π(7r)2 = 49πr2 — площадь увеличится в 49 раз.
541. а) да; б) нет.
543. а) 28 • 57 = 2 • (2 • 5)7 = 2 • 107 ⇒ 107 < 28 • 57 б) 213 • 311 = 22 • (2 • 3)11 = 4 • 611; 612 = 6 • 611 ⇒ 612 > 213 • 311 в) 2525 = 52 • 25 = 550; 250 • 350 = (2 • 3)50 = 650 ⇒ 2525 < 250 • 350 г) 6330 = (9 • 7)30 = 360 • 730 ⇒ 6330 > 360 • 530 544. а) (-33)2 = 36; б) (-32)3 = -36; в) -(34)2 = -38; г) -(-32)3 = 36. 545. а) (x3)2 • (-x3)4 = x3 • 2 x3 • 4 = x6 • x12 = x18; б) (-у3)7 • (-у4)5 = -у3 • 7 • (-у4 • 5) = у21 • у20 = у41; в) (x7)5 • (-x2)6 = x7 • 5 • x2 • 6 = x35 • x12 = x47; г) (-с9)4 • (с5)2 = с9 • 4 • с5 • 2 = с36 • с10 = с46. 546. а) р5 = x20 ⇒ р = x(20 : 5) = x4; б) р7 = x21 ⇒ р = x(21:7) = x3; в) р3с8 = с20 ⇒p = 547. а) 45 • 221 = (22)5 • 221 = 210 • 221 = 231; б) 2513 : 511 = (52)13 : 511 = 526 : 511 = 526 - 11 = 515;. в) 85 • 1613 = (23)5 • (24)13 = 215 • 252 = 267; г) 2710 : 915 = (33)10 : (32)15 = 330 : 330 = 30. 548. а) (-x3)7 = -x3 • 7 = -x21; б) (-x2)5 = -x2 • 5 = -x10; в) (-x)4x8 = x4 + 8 = x12; г) (-x5)7 • (x2)3 = = -x35 • x6 = -x41. 549. а) Разложим 15 на простые множители: 15 = 3 • 5 ⇒ 215 = (23)5 = (25)3. Ответ: двумя способами. б) Разложим 6 на простые множители: 6 = 3 • 2 ⇒ 26 = (23)2 = (22)3. Ответ: двумя способами. 550. а) х2 + у2 = 0 — при х = у = 0; б) (х + у)2 = 0 — при x = -у. 551. Так как единица в любой натуральной степени равняется самой себе, значит и число а в любой натурально степени будет заканчиваться на 1. Аналогичное свойство выполняется для цифр: 0; 5; 6. 552. a) 34k = (34)k = 81k — так как единица в любой натуральной степени равняется самой себе, значит и число 81k в любой натурально степени будет заканчиваться на 1; б) 10k - 1: 10k — состоит из единицы и к нулей; 10k - 1 — состоит из к девяток, значит кратно 3.
|
|
|



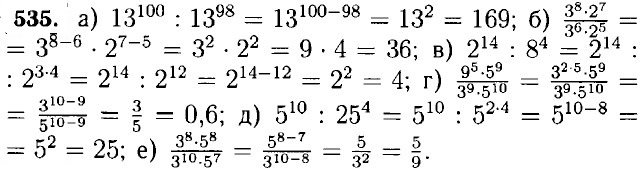
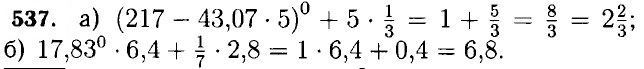
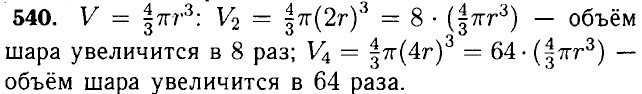
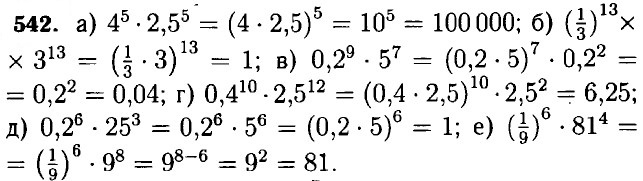
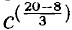 = c4; г) у7 • (у2)4 = р5 ⇒ у7 • (у2)4 ⇒ у7 • у2 • 4 = у7 • y8 = у15 ⇒ р = у(15 : 5) = у3.
= c4; г) у7 • (у2)4 = р5 ⇒ у7 • (у2)4 ⇒ у7 • у2 • 4 = у7 • y8 = у15 ⇒ р = у(15 : 5) = у3.