|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений Дополнительные упражнения к параграфу 7511. а) 32 + 42 + 52 = 9 + 16 + 25 = 50 ≠ 62 — не верно; б) (1 + 2 + 3 + 4)2 = 102 = 100; 1 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100; (1 + 2 + 3 + 4)2 = 1 +23 + 33 + 43 - верно. 512. 267+ 155 - 119: 267 — последняя цифра 6; 119 — последняя цифра 1; 155 — последняя цифра 5; 6 + 5 - 1 = 10; 267 + 155 - 119 — оканчивается цифрой 0, значит кратно 10. 513. а) 54 = 2 • 33; б) 144 = 24 • 32; в) 225 = 32 • 52; г) 500 = 22 • 53. 514. а) 64 = 26; б) 81 = 34; в) 512 = 29; г) 729 = 36; д) 1024 = 210. 515. а) 6 = 22 + 2; б) 18 = 24 + 2; в) 42 = 25 + 10 = 25 + 23 + 2. 51б. а) 121 = 112; б) -32 = (-2)5; в) 0,125 = (0,5)3; г) 625 = 54; д) -0,216 = (-0,6)3; е) 0,343 = 0,73. 517. а) при х = -2; 0,001x2 = 0,001 • (-2)2 = 0,001 • 4 = 0,004; б) при у = 0,1; 1000у3 = 1000 • 0,13 = 1000 • 0,001 = 1; в) при х = 5, у = 2; x2у4 = 5224 = 25 • 16 = 400; г) при х = -2, у = -5; 3х3y3 = 3 • (-2)3 • (-5)3 = 3 • 8 • 125 = 3000. 518. (-1)n: а) при n = 6 (-1)n = 1; б) при n = 11 (-1)n = -1; в) при n = 23 (-1)n = -1; г) при n = 70 (-1)n = 1. 519. а) 53 + (-3)3 = 125 - 27 = 98; б) (9 - 11)3 = (-2)3 = -8; в) 122 - 82 = 144 - 64 = 80; г) (96 - (-4))2 = 1002 = 10000; д) 2 • 72 • (-5)2 = 2 • 49 • 25 = 2450; е) 3 • 15 • 42 = 3 • 15 • 16 = 720. 520. а) (-0,03)8 = 0,0038 > 0; б) (-1,25)7 = -1,257 < 0; в) (-1,75)3 = -1,753; (-0,29)2 = 0,292 ⇒ (-1,75)3 < (-0,29)2; г) 0,986 < 1,026. 521. а) 23 = 8; 32 = 9; 9 - 8 = 1 ⇒ 23 < 32; 32 больше на 1. б) 52 = 25; 25 = 32; 32 - 25 = 7 ⇒ 52 < 25; 25 больше на 7. в) 2 • 32 = 2 • 9 = 18; 3 • 23; = 3 • 8 - 24; 24 - 18 = 6 ⇒ 2 • 32 < 3 • 23; 3 • 23 больше на 6. г) (11 + 19)2 = 302 = 900; 112 + 192 = 121 + 361 = 482; 900 - 482 = 418 ⇒ (11 + 19)2 > 112 + 192; (11 + 19)2 больше на 418. 522. а) (-12)2 = 122; (-12)3 = -123 ⇒ (-12)2 > (-12)3; б) 02 = 03; в) 52 < 53. 523. а) при х = 1,5: х2 = (-х)2 = 2,25; -х2 = -2,25. при х = -2: х2 = (-x) = 4; -х2 = -4. б) при х = 1,5: х3 = 3,375; -х3 = (-х)3 = -3,375; при х = -2: х3 = -8; -х3 = (-х)3 = 8. 524. Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9. Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. а) б) в) 525. х ∈ {-3; -2; -1; 1; 2; 3}: а) х4 = 81 ⇒ х = ±3; б) х6 = 64 ⇒ х = ±2; в) x2 - х = 2 ⇒ х = -1 или х = 2; г) х4 + х3 = 6х2 ⇒ х = -3 или х = 2; д) х3 - 3х2 — 4х + 12 = 0 ⇒ х = -2; х = 2 или х = 3; е) х3 + 3х2 - х - 3 = 0 ⇒ х = -3; х = -1 или х = 1. 526. а) х2 +1 = 0 ⇒ х2 = -1 — не имеет корней, так как квадрат любого числа не отрицательное число; б) 2х6 + 3х4 + х2 + 1 = 0 ⇒ 2х6 + 3х4 + х2 = -1 — в правой части равенства переменные с чётными показателями, поэтому правая часть не отрицательная, значит уравнение не имеет корней. 527. (2х + 3)2 = 0 ⇒ 2х + 3 = 0 ⇒ 2х = -3 ⇒ х = -1,5. 528. х4 + 3х3 + 2х2 + х + 6 = 0 ⇒ х4 + 3х3 + 2х2 + х = -6 — при х > 0, х4 > 0; 3х3 > 0; 2х2 > 0; х > 0. В левой части равенства сумма чисел больше нуля, а в правой отрицательное число, значит уравнение х4 + 3х3 + 2х2 + х + 6 = 0 не имеет положительных корней. <<< К началу Решенния (окончание) >>>
|
|
|



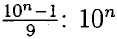 — состоит из единицы и п нулей; 10n - 1 — состоит из n девяток, Значит
— состоит из единицы и п нулей; 10n - 1 — состоит из n девяток, Значит 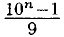 делится на 9 без остатка.
делится на 9 без остатка.
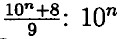 — состоит из единицы и n нулей; 10n + 8 — состоит из одной единице, n - 1 нулей и 8, сумма цифр равна 9, значит
— состоит из единицы и n нулей; 10n + 8 — состоит из одной единице, n - 1 нулей и 8, сумма цифр равна 9, значит 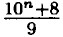 — делится на 9 без остатка.
— делится на 9 без остатка.
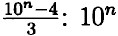 — состоит из единицы и n нулей; 10n - 4 — состоит из n - 2 девяток, и 6, сумма цифр кратна 3, значит
— состоит из единицы и n нулей; 10n - 4 — состоит из n - 2 девяток, и 6, сумма цифр кратна 3, значит 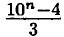 — делится на 9 без остатка.
— делится на 9 без остатка.