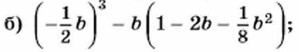|
|
|
|
|
§ 10. Произведение одночлена и многочлена Умножение одночлена на многочлен (продолжение)618. Упростите выражение и найдите ого значение: а) 3(2x - 1) + 5(3 - x) при x = -1,5; б) 25а - 4(3а - 1) + 7(5 - 2а) при а = 11; в) 4у - 2(10y - 1) + (8у - 2) при у = -0,1; г) 12(2 - 3р) + 35р - 9 (р + 1) при р = 2. 619. Представьте в виде многочлена:
620. Упростите выражение:
621. Представьте в виде многочлена:
622. Найдите значение выражения: а) -2х(х2 - х + 3) + x(2х2 + х - 5) при х = 3; -3; б) x(x - у) - у(у2 - х) при х = 4 и у = 2. 623. Вычислите значение выражения: а) 5дг(2х - 6) - 2,5х(4х - 2) при х = -8; 10; б) 5а(а - 4b) - 4b(b - 5а) при а = -0,6 и b = -0,5. 624. Упростите выражение:
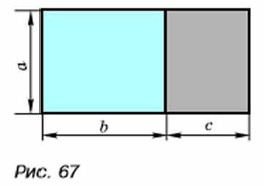
в) х(16x - 2x3) - (2x2)2; г) (0,2с3)2 - 0,01с4 (4с2 - 100). 625. С помощью рисунка 67 разъясните геометрический смысл формулы а(b + с) = аb + ас для положительных значений а, b и с.
626. Докюките, что выражение х(2х + 1) - х2(х + 2) + (x3 - х + 3) при любом значении х принимает одно и то же значение. 627. Докажите, что значение выражения у(3у2 - у + 5) - (2у3 + 3 у- 16) - у(у2 - у + 2) не зависит от у. 628. Докажите, что выражение тождественно равно нулю: а) а(b - с) + b(с - а) + с(а - b); б) а(b + с - bс) - b(с + а - ас) + с(b - а). 629. Докажите, что выражение 2х(х - 6) - 3(х2 - 4х + 1) при любых значениях х принимает отрицательные значения. 630. Решите уравнение:
631. Найдите корень уравнения: а) 3х(2х - 1) - 6х(7 + х) = 90; б) 1,5x(3 + 2х) = 3х(х + 1) - 30; в) 5x(12x - 7) - 4x(15х - 11) = 30 + 29x; г) 24x - 6x(13х - 9) = -13 - 13x(6x - 1). 632. Решите уравнение: а) 3(-2x + 1) - 2(x + 13) = 7x - 4(1 - x); б) -4(5 - 2а) + 3(а - 4) = 6(2 - а) - 5а; в) 3у(4у - 1) - 2у(6y - 5) = 9у - 8(3 + у); г) 15x + 6x(2 - 3х) = 9х (5 - 2x) - 36.
|
|
|