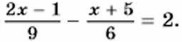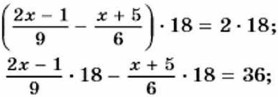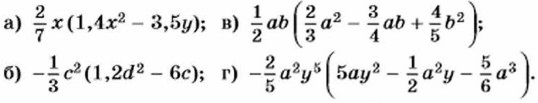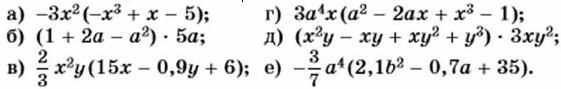Умножение одночлена на многочлен

Умножим одночлен 9n³ на многочлен 7n² - 3n + 4.

Для этого составим их произведение и преобразуем его, используя распределительное свойство умножения. Умножая одночлен на каждый член многочлена и складывая результаты, получим

9n³(7n² - 3n + 4) = 9n³ • 7n² - 9n³ • 3n + 9л³ • 4 = 63n⁵ - 27n⁴ + 36n³.

Произведение одночлена 9n³ и многочлена 7n² - 3n + 4 мы представили в виде многочлена 63n⁵ - 27n⁴ + 36n³.

Вообще произведение одночлена и многочлена всегда можно представить в виде многочлена. При умножении одночлена на многочлен пользуются правилом:

чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Пример 1. Умножим одночлен -3а² на многочлен 4а³ - а + 1.

Воспользуемся правилом умножения одночлена на многочлен:

-3а²(4а³ - а + 1) = -3а² • 4а³ - 3а² • (-а) - 3а² • 1 = -12а⁵ + 3а³ - 3а².

Заметим, что запись можно вести короче, не выписывая промежуточные результаты:

-3а²(4а³ - а + 1) = -12а⁵ + 3а³ - 3а².

Пример 2. Упростим выражение 3x² - 2x(x + 8).

3х² - 2х(х + 8) = 3x² - 2х² - 16x = х² - 16x.

Умножение одночлена на многочлен часто применяется при решении уравнений.

Пример 3. Решим уравнение 8 - 5x(x - 7) = 1 - 5x².

Имеем

8 - 5x(x - 7) = 1 - 5x²;

8 - 5x2 + 35x = 1 - 5x2;

-5x² + 35x + 5x² =1 - 8;

35x = -7;

x = -0,2.

Пример 4. Решим уравнение

Умножим обе части уравнения на наименьшее общее кратное знаменателей дробей, т. е. на число 1В:

2(2x - 1) - 3(x + 5) = 36;

4x - 2 - 3x - 15 = 36;

x = 53.

Упражнения

614. Выполните умножение:

а) 2x(x² - 7x - 3);
б) -4b²(5b² - 3b - 2);
в) (3а³ - а² + а)(-5а³);

г) (у² - 2,4y + 6) • 1,5y;
д) -0,5x²(-2x² - 3x + 4);
е) (-3у² + 0,6.у)(-1,5y³).

615. Преобразуйте произведение в многочлен:

а) 3ab(a² - 2ab + b²);
б) -x²y/(x²y² - x² - y²);
в) 2,5а²b(4а² - 2аb + 0,2b²);

г) (-2аx² + 3аx - 2^{) (-а²x²);}
д) (6,3x³y - 3у² - 0,7x) • 10x²y²;
е) -1,4p²q⁶(5p³q - 1,5pq² - 2q³).

616. Представьте в виде многочлена:

617. Выполните умножение:

Продолжение >>>