|
|
|
|
√лавна€ >> ƒомашние работы к учебнику ћакарычева. јлгебра 7 класс |
|
|
–ешенни€ упражнений ”множение одночлена на многочлен614. а) 2х Х (х2 - 7х - 3) = 2х Х х2 - 2х Х 7х - 2х Х 3 = 2x3 - 14x2 - 6x; б) -4b2 Х (5b2 - 3b - 2) = -4b2 Х 5b2 + 4b2 Х 3b + 4b2 Х 2 = -20b4 + 12b3 + 8b2; в) (3а3 - а2 + а)(-5а3) = -3а3 Х 5а3 + а2 Х 5а3 - а Х 5а3 = -15а6 + 5а5 - 5а4; г) (у2 - 2,4у + 6) Х 1,5у = у2 Х 1,5у - 2,4у Х 1,5у + 6 Х 1,5у = 1,5у3 - 3,6у2 + 9у; д) Ч0,5x2 Х (-2x2 - 3x + 4) = 0,5х2 Х 2х2 + 0,5x2 Х 3x - 0,5x2 Х 4 = x4 + 1,5х3 - 2x2; е) (-3у2 + 0,6у)(-1,5у3) = 3у2 Х 1,5у3 - 0,6у Х 1,5у3 = 4,5у5 - 0,9у4. 615. а) 3аb Х (а2 - 2аb + b2) = 3аb Х а2 - 3аb Х 2аb + 3аb Х b2 = 3а3b - 6а2b2 + 3аb3; б) -х2у Х (х2у2 - х2 - у2) = -х2у Х х2у2 + х2у Х х2 + х2у Х у2 = -х4у3 + х4у + х2у3; в) 2,5а2b Х (4а2 - 2аb + 0,2b2) = 2,5а2b Х 4а2 - 2,5а2b Х 2аb + 2,5а2b Х 0,2b2 = 10а4b - 5а3b2 + 0,5а2b3; г) (-2ах2 + 3ах - а2)(-а2х2) = 2ах2 Х а2x2 - 3аx Х а2х2 + а2 Х а2х2 = 2а3х4 - 3а3х3 + а4х2; д) (6,3х3у - 3у2 - 0,7х) Х 10х2у2 = 6,3х3у Х 10x2у2 - 3у2 Х 10x2у2 - 0, 7х Х 10х2у2 = 63х5у3 - 30х2у4 - 7х3у2; е) -1,4p2q6 Х (5p3q - 1,5pq2 - 2q3) = -1,4p2y6 Х 5p3q + 1,4p2q6 Х 1,5pq2 + 1,4p2q6 Х 2q3 = -7p5q7 + 2,1p3q8 + 2,8p2q9.
618. а) 3 Х (2х - 1) + 5 Х (3 - х) = 6х - 3 + 15 - 5х = (6х - 5х) + (-3 + 15) = х + 12: при х = -1,5 ⇒ х + 12 = -1,5 + 12 = 10,5. б) 25а - 4 Х (3а - 1) + 7 Х (5 - 2а) = 25а - 12а + 4 + 35 - 14а = (25а - 12а - 14а) + (4 + 35) = -а + 39: при а = 11 ⇒ -а + 39 = -11 + 39 = 28. в) 4у - 2 Х (10у - 1) + (8у - 2) = 4у - 20у + 2 + 8у - 2 = (4у - 20у + 8у) + (2 - 2) = -8у: при у = -0,1 ⇒ -8у = -8 Х (-0,1) = 0,8. г) 12 Х (2 - 3р) + 35р - 9 Х (р + 1) = 24 - 36р + 35р - 9р - 9 = (-36р + 35р - 9р) + (24 - 9) = -10р + 15: при р = 2 ⇒ -10p + 15 = -10 Х 2 + 15 = -20 + 15 = -5. 619. а) 14b + 1 - 6 Х (2 - 11b) - 14b + 1 - 12 + 66b = (14b + 66b) + (1 - 12) = 80b - 11; б) 25 Х (2 - 3с) + 16 Х (5с - 1) = 50 - 75с + 80с - 16 = (-75с + 80с) + (50 - 16) = 5с + 34; в) 14 Х (7х - 1) - 7 Х (14х + 1) = 14 Х 7х - 14 - 7 Х 14х - 7 = (14 Х 7х - 7 Х 14х) + (-14 - 7) = -21; г) 36 Х (2 - у) - 6 Х (5 - 2у) = 6 Х (12 - 6y - 5 + 2у) = 6 Х (7 - 4у) = 42 - 24y. 620. а) 14у + 2у Х (6 - у) - 14у + 12y - 2у2 = 2bу - 2у2; б) 3у2 - 2у Х (5 + 2у) = 3у2 - 10у - 4у2 = -10y - у2; в) 4х Х (х - 1) - 2 Х (2х2 - 1) = 4х2 - 4х - 4х2 + 2 = -4х + 2; г) 5а Х (а2 - 3а) - 3а Х (а2 - 5а) = 5а3 - 15а2 - 3а3 + 15а2 = 2а3; д) 7b Х (4с - b) + 4с Х (с - 7b) = 28bс - 7b2 + 4с2 - 28bс = -7b2 + 4с2; е) - 2у Х (х3 - 2у) - (х3у + 4у2) = -2х3у + 4у2 - х3у - 4у2 = -3х3у; ж) 3m2 Х (m + 5n) - 2а Х (8m2 - n) = 3m3 + 15m2n - 16m2n + 2n2 = 3m3 - m2n + 2n2; з) 6m2n3 - n2 Х (6m2n + n - 1) = 6m2n3 - 6m2n3 - n3 + n2 = -n3 + n2. 621. а) 6х Х (х Ч 3) Ч х Х (2 Ч х) = 6х2 Ч 18х Ч 2х + х2 == 7х2 Ч 20х; б) -а2 Х (3а - 5) + 4а Х (а2 - а) = -3а3 + 5а2 + 4а3 - 4а2 = а3 + а2; в) ах Х (2х - 3а) - х Х (ах + 5а2) = 2ах2 - 3а2х - ах2 - 5а2х = ах2 - 8а2х; г) - 4m2 Х (n2 - m2) + 3n2 Х (m2 - n2) = -4m2n2 + 4m4 + 3m2n2 - 3n4 = 4m4 - m2n2 - 3n4. 622. а) -2х Х (х2 - х + 3) + х Х (2х2 + х - 5) = -2х3 + 2х2 - 6х + 2х3 + х2 - 5х = 3х2 - 11х: при х = 3 ⇒ 3х2 - 11х = 3 Х 32 - 11 Х 3 = 27 - 33 = -6; при х= -3 ⇒ 3х2 - 11х = 3 Х (-3)2 - 11 Х (-3) = 27 + 33 = 60. б) х Х (х - у) - у Х (у2 - х) = х2 - ху - у3 + ху = х2 - у3: при х = 4 и у = 2 ⇒ х2 - у3 = 42 - 23 = 16 - 8 = 8. 623. а) 5х Х (2х - 6) - 2,5х Х (4х - 2) = 10х2 - 30х - 10х2 + 5х = -25х: при х = -8 ⇒ -25х = - (-8) = 200; при х = 10 ⇒ -25х = -25 Х 10 = -250. б) 5а Х (а - 4b) - 4b Х (b - 5а) = 5а2 - 20аb - 4b2 + 20аb = 5а2 - 4b2: при а = -0,6 и b = -0,5 ⇒ 5а2 - 4b2 = 5 Х (-0,6)2 - 4 Х (-0,5)2 = 5 Х 0,36 - 4 Х 0,25 = 1,8 - 1 = 0,8. 624. а) (3а2)2 - а3 Х (1 - 5а) = 32а2 Х 2 - а3 + 5а4 = 9а4 - а3 + 5а4 = 14а4 - а3; б) 625. ab Ч площадь оранжевого пр€моугольника, ас Ч площадь серого пр€моугольника, ab + ac Ч сумма площадей оранжевого и серого пр€моугольников, ab + ac = а - (b +с) Ч площадь пр€моугольника со сторонами а и b + с. 626. х Х (2х + 1) - х2 Х (х + 2) + (х3 - х + 3) = 2х2 + х - х3 - 2х2 + x3 Ч х + 3 = (2х2 - 2х2) + (х - х) + (-x3 + х3) + 3 = 3 Ч значение выражени€ не зависит от х. 627. у Х (3у2 - у + 5) - (2у3 + 3у -16) - у Х (у2 - у + 2) = 3у3 - y2 + 5у - 2у3 - 3у + 16 - у3 + у2 - 2у = (3у3 - 2у3 - у3) + (-y2 + y2) + (5y - 3y - 2у) + 16 = 16 Ч значение выражени€ не зависит от у. 628. а) а Х (b - с) + b Х (с - а) + с Х (а - b) = ab - ac + bc - ab + ac - bc = 0; б) а Х (b + с - bc) - b Х (с + а - ас) + с Х (b - а) - ab + ас - abc - bc - ab + abc + cb Ч ac = 0. 629. 2х Х (х - 6) - 3 Х (х2 - 4х + 1) = 2х2 - 12х - 3х2 + 12х - 3 = -х2 - 3, т. к. х2 ≥ 0, то х2 ≤ 0, значит -х2 - 3 ≤ -3 Ч при любых значени€х х принимает отрицательные значени€. 630. а) 5х + 3 Х (х - 1) = 6x + 11 ⇒ 5х + 3х - 3 = 6x + 11 ⇒ 8х - 6x = 11 + 3 ⇒ 2х = 14 ⇒ х = 7; б) 3х - 5 Х (2 - х) = 54 ⇒ 3х - 10 + 5х = 54 ⇒ 8x = 64 ⇒ x = 8; в) 8 Х (у - 7) - 3 Х (2у + 9) = 15 ⇒ 8у - 56 - 6у - 27 = 15 ⇒ 2у = 15 + 56 + 27 ⇒ 2у = 98 ⇒ у = 49; г) 0,6 - 0,5 Х (у - 1) = у + 0,5 ⇒ 0,6 - 0,5у + 0,5 = у + 0,5 ⇒ 1,5у - 0,6 ⇒ у Ч 0,4; д) 6 + (2 - 4х) + 5 = 3 Х (1 - 3x) ⇒ 6 + 2 - 4х + 5 = 3 - 9x ⇒ 9x - 4х = 3 - 6 - 2 - 5 ⇒ 5x = -10 ⇒ х = -2; ж) 0,15 Х (x - 4) = 9,9 - 0,3 Х (x - 1) ⇒ 0,15x - 0,6 = 9,9 - 0,3x + 0,3 ⇒ 0,15x + 0,3x = 9,9 + 0,3 + 0,6 ⇒ 0,45x = 10,8 ⇒ x = 24; з) 3 Х (3x - 1)+2 = 5 Х (1 -2х) -1 ⇒ 9х - 3 + 2 = 5 - 10х - 1 ⇒ 9х + 10х = 5 - 1 - 2 + 3 ⇒ 19x = 5 ⇒ х = 631. а) 3x Х (2x - 1) - 6x Х (7 + х) - 90 ⇒ бх2 - 3x - 42х - 6x2 = 90 ⇒ -45х = 90 ⇒ х = -2; б) 1,5х Х (3 + 2x) = 3x Х (х + 1) - 30 ⇒ 4,5х + 3х2 = 3х2 + 3х - 30 ⇒ 4,5х - 3х + 3х2 - 3х2 = -30 ⇒ 1,5х = -30 ⇒ х = -20; в) 5х Х (12х - 7) - 4х Х (15х - 11) = 30 + 29х ⇒ 60х2 - 35х - 60х2 + 44х = 30 + 29х ⇒ -35х + 44х - 29х = 30 ⇒ -20х = 30 ⇒ х = -1,5; г) 24х - 6х Х (13х - 9) = -13 - 13х Х (6х - 1) ⇒ 24х - 78х2 + 54х = -13 - 78х2 + 13х ⇒ 24х + 54х - 13х - 78х2 + 78х2 = -13 =+ 65х = -13 ⇒ х = -0,2. 632. а) 3 - (-2х + 1) - 2 Х (х + 13) = 7х - 4 Х (1 - х) ⇒ ⇒ -6х + 3 - 2х - 26 = 7х - 4 + 4х ⇒ 7х + 4х + бх + 2х = -26 + 3 + 4 ⇒ 19х = -19 ⇒ х = -1; б) -4 Х (5 - 2а) + 3 Х (а - 4) = 6 Х (2 - а) - 5а ⇒ -20 + 8а + 3а - 12 = 12 - 6а - 5а 8а + 3а + 6а + 5а = 12 + 20 + 12 ⇒ 22а = 44 ⇒ а = 2; в) 3у Х (4у - 1) - 2у Х (6у - 5) = 9у - 8 Х (3 + у) ⇒ 12у2 - 3у - 12у2 + 10 у = 9у - 24 - 8у ⇒ -3 у + 10у - 9 у + 8у = -24 ⇒ 6у = -24 ⇒ у = -4; г) 15х + 6х Х (2 - 3х) = 9х Х (5 - 2х) - 36 ⇒ 15х + 12х - 18х2 = 45х - 18х2 - 36 ⇒ 15х + 12х - 45х - 18х2 + 18х2 = -36 ⇒ -18х = -36 ⇒ х = 2. <<< началу –ешенни€ (окончание) >>>
|
|
|



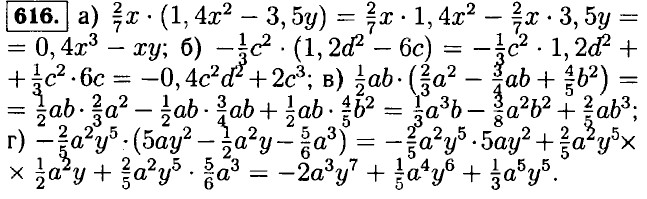
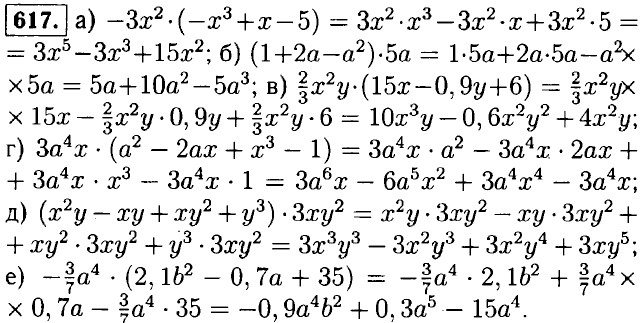
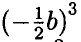 - b Х (1 - 2b -
- b Х (1 - 2b - 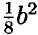 ) =
) = 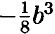 - b + 2b2 +
- b + 2b2 + 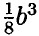 = 2b2 - b; в) х Х (16х - 2х3) - (2х2)2 = 16х2 - 2х4 - 4х4 = 16х2 - 6х4; г) (0,2с3)2 - 0,01с4 Х (4с2 - 100) = 0,04с6 - 0,04с6 + с4 = с4.
= 2b2 - b; в) х Х (16х - 2х3) - (2х2)2 = 16х2 - 2х4 - 4х4 = 16х2 - 6х4; г) (0,2с3)2 - 0,01с4 Х (4с2 - 100) = 0,04с6 - 0,04с6 + с4 = с4.