|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Домашние работы Умножение одночлена на многочлен (окончание)633. а) 2 • (3 - 5с) + 1 = 4 • (1 - с) ⇒ 6 - 10с + 1 = 4 - 4с ⇒ 10с - 4с = 6 + 1 - 4 ⇒ 6с = 3 ⇒ с = 0,5; б) -3 • (2х + 1) = 8х + 5 + 20 ⇒ -6х - 3 = 8х + 25 = 4 ⇒ -бх - 8х = 25 + 3 ⇒ -14х - 28 ⇒ х = -2; в) 3 • (5х + 7) = 61 - 10х ⇒ 15х + 21 = 61 - 10х ⇒ 15х + 10х = 61 - 21 ⇒ 25х = 40 ⇒ х = 1,6; г) 8 - у = 2 • (7 + у) ⇒ 8 - у = 14 + 2у ⇒ 2у + у - 8 - 14 ⇒ 3 у = -6 ⇒ у = -2. 634. б) в) г) д) е) ж) з) и)
639. Периметр треугольника 44 см. Одна из его сторон равна 2х, тогда вторая 2х + 4 и третья х. Значит 2x + 2x + 4 + x = 44 ⇒ 5x = 40 ⇒ x = 8 ⇒ 2x = 16 ⇒ 2x + 4 = 20. Ответ: 20 см 16 см и 8 см. 640. Пусть площадь одного из них 1,5x, тогда площадь второго х и площадь третьего 1,5x + 6, Значит 166 = 1,5x + x + 1,5x + б ⇒ 4х = 160 ⇒ x = 40 ⇒ 1,5x = 60 ⇒ 1,5x + 6 = 66. Ответ: 40 м2, 60 м2 и 66 м2.
642. Пусть во втором сарае было х т сена, тогда в первом 3? т. Значит 643. Пусть бригада должна была скосить луг за n дней. Тогда площадь луга равна 50n. Значит 60 • (n - 1) = 50n ⇒ 60n - 60 = 50n ⇒ 10n = 60 ⇒ n = 6 ⇒ 50n = 300. Ответ: 300 га. 644. Пусть спортсменка с первоначальной скоростью пробегала дистанцию за t мин. Тогда длина дистанции равна 250t м. Значит 250t = 300 • (t - 1) ⇒ 200t = 300t - 300 ⇒ 50t = 300 ⇒ t = 6 ⇒ 250t = 1500. Ответ: длина дистанции 1500 метров. 645. Пусть туристы затратили на путь от турбазы до привала t ч. Значит расстояние от турбазы до привала 4,5t. 15 мин = 0,25 ч. Значит 4,5t = 4 • (t + 0,25) ⇒ 4,5t = 4t + 1 ⇒ 0,5t = 1 ⇒ t = 2 ⇒ 4,5t = 9. Ответ: На расстоянии 9 км от тур базы был сделан привал. 646. Пусть мотоциклист догонит велосипедиста за t часов. Тогда велосипедист проедет 12* км. Значит 12t + 60 = 30t ⇒ 18t = 60 ⇒ t = 647. Пусть легковая машина догонит грузовую за t ч. Тогда грузовая машина пройдёт путь 60t. Значит 60t = 90 • (t - 2) ⇒ 60t = 90t - 180 ⇒ 30t = 180 ⇒ t = 6 ⇒ 60t = 360. Ответ: На расстоянии 360 км от пункта А легковая машина догонит грузовую.
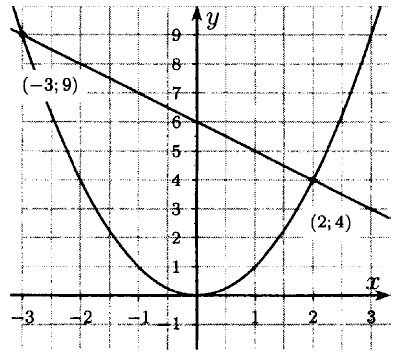
650. а) у = 5х + 29 и у = -3х - 11 ⇒ 5x + 29 = -3х - 11 ⇒ 8x = -40 ⇒ х = -5 ⇒ у = -3х - 11 = 15 - 11 = 4 ⇒ (-5; 4) — координаты точки пересечения. б) у = 1,2х и у = 1,8х + 9,3 ⇒ 1,2x = 1,8х + 9,3 ⇒ 0,6х = -9,3 ⇒ х = -15,5 ⇒ у = 1,2x = 1,2 • (-15,5) = -18,6 ⇒ (-15,5; -18,6) — координаты точки пересечения. 651. а) 2 и 4; б) 1, 2 и 4; в) 1 и 3; г) 1, 3, и 4. 652. х = 2; х = -3.
|
|
|



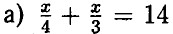 — умножим обе части на 12 ⇒ 3x + 4х = 3 • 4 • 14 ⇒ 7х — 168 ⇒ х = 24;
— умножим обе части на 12 ⇒ 3x + 4х = 3 • 4 • 14 ⇒ 7х — 168 ⇒ х = 24;
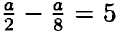 — умножим обе части на 8 ⇒ 4а - а = 5 • 8 ⇒ 3а = 40 ⇒ а =
— умножим обе части на 8 ⇒ 4а - а = 5 • 8 ⇒ 3а = 40 ⇒ а = 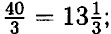
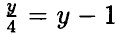 — умножим обе части на 4 ⇒ у = 4у - 4 ⇒ 3у = 4 ⇒ у =
— умножим обе части на 4 ⇒ у = 4у - 4 ⇒ 3у = 4 ⇒ у = 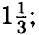
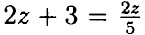 ~ умножим обе части на 5 ⇒ 10z + 15 = 2z ⇒ 8z = -15 ⇒ z =
~ умножим обе части на 5 ⇒ 10z + 15 = 2z ⇒ 8z = -15 ⇒ z = 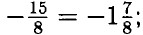
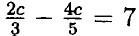 — умножим обе части на 15 ⇒ 10с - 12с = 15 • 7 ⇒ -2с = 105 ⇒ с = -52,5;
— умножим обе части на 15 ⇒ 10с - 12с = 15 • 7 ⇒ -2с = 105 ⇒ с = -52,5;
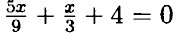 — умножим обе части на 9 ⇒ 5х + 3х + 36 = 0 ⇒ 8х = -36 ⇒ х = -4,5;
— умножим обе части на 9 ⇒ 5х + 3х + 36 = 0 ⇒ 8х = -36 ⇒ х = -4,5;
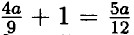 — умножим обе части на 36 ⇒ 16а + 36 = 15а ⇒ а = -36;
— умножим обе части на 36 ⇒ 16а + 36 = 15а ⇒ а = -36;
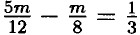 — Умножим обе части на 24 ⇒ 10m - 3m = 8 ⇒ 7m = 8 ⇒ m =
— Умножим обе части на 24 ⇒ 10m - 3m = 8 ⇒ 7m = 8 ⇒ m = 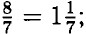
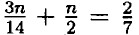 — умножим обе части на 14 ⇒ 3n + 7n = 4 ⇒ 10n = 4 ⇒ n = 0,4.
— умножим обе части на 14 ⇒ 3n + 7n = 4 ⇒ 10n = 4 ⇒ n = 0,4.

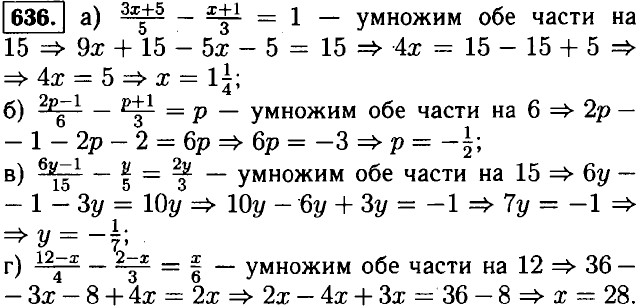
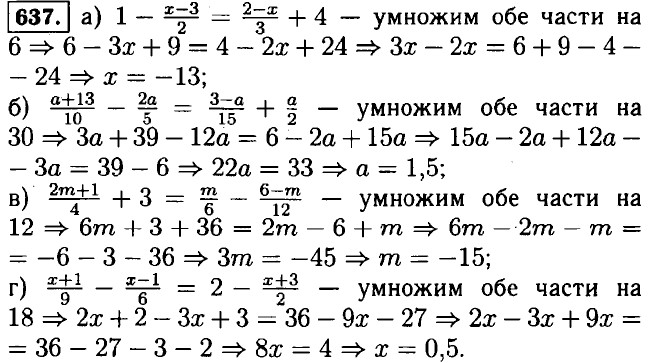


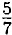 (3x - 2) = х + 2 ⇒ 1бx - 10 = 7x + 14 ⇒ 8x = 24 ⇒ x = 3 ⇒ 3x = 9. Ответ: в первом сарае было 3 т сена, во втором 9 т.
(3x - 2) = х + 2 ⇒ 1бx - 10 = 7x + 14 ⇒ 8x = 24 ⇒ x = 3 ⇒ 3x = 9. Ответ: в первом сарае было 3 т сена, во втором 9 т.
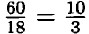 ⇒ 12t = 12 •
⇒ 12t = 12 • 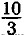 = 40. Ответ: 40 км.
= 40. Ответ: 40 км.