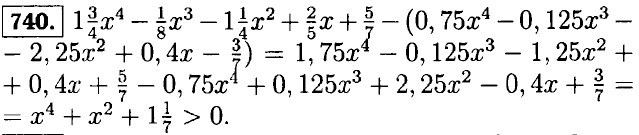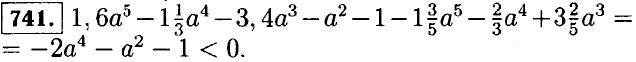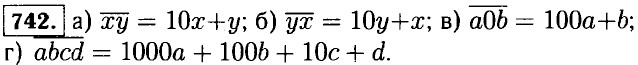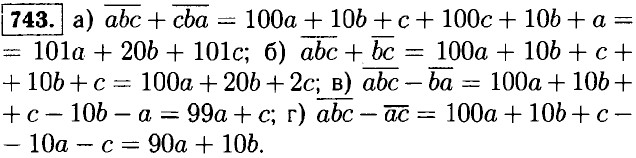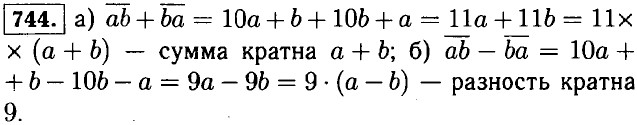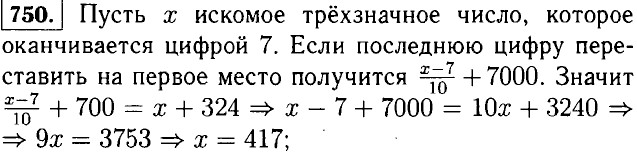Дополнительные упражнения к параграфу 9

734. а) 2x² + 6x = 2 • (х + 3) — при любом значении х является чётным. В результате сложения чётного и не чётного получится не чётное число. Ответ: не при каких х, значение выражения не окажется чётным числом.

б) х² + х при чётном х является чётным, при нечётном х, так же является чётным, так как сумма двух нечётных чисел чётна. х² + х + 2 в результате суммы двух чётных чисел получится чётное число. Ответ: не при каких х, значение выражения не окажется не чётным числом.

735. а) 8а² - 6а³х + 3ах² - х³; б) -6а³х + 8а² + 3ах² - x³.

736. а) (-2х² + х + 1) - (х² - х + 7) - (4х² + 2х + 8) = -2х² + х + 1 - х² + х - 7 - 4х² - 2х - 8 = -7х² - 14; б) (3а² - а + 2) + (-3а² + 3а - 1) - (а² - 1) = 3а² - а + 2 - 3а² + 3а - 1 - а² + 1 = -а² + 2а + 2; в) 2а - 3b + с - (4а + 7b + с + 3) = 2а - 3b + с - 4а - 7b - с - 3 = -2а -10b - 3; г) 2ху - у² + (у² - ху) - (х² + ху) = 2ху - у² + у² - ху - х² - ху = -х².

737. a) (1 - х + 4x² — 8x³) + (2x³ + х² - 6x - 3) - (5x³ + 8x²) = 1 - х + 4х² - 8х³ + 2х³ + х² - 6x - 3 - 5x3 - 8x² = -11x³ - 3x² - 7х - 2; б) (0,5а - 0,6b + 5,5) - (-0,5а + 0,4b) + (1,3b - 4,5) = 0,5а - 0,6b + 5,5 + 0,5а - 0,4b + 1,3b - 4,5 - а + 0,36 + 1.

738. если А = 2x - 1; В = 3х + 1; С = 5x, то A + B - С = 2х - 1 + 3x + 1 - 5x = 0 и С - В - А = 5х - 3х - 1 - 2x + 1 = 0, значит А + В - С = С - В - А.

739. а) (у² - 5у + 1) - 0 = у² - 5у + 1; б) (у² - 5у + 1) - 5 = у² - 5у + 1 - 5 = у² - 5у - 4; в) (у² - 5у + 1) - у² = -5у + 1; г) (у² - 5у + 1) - (4у² - у + 7) = у² - 4у² - 5у + у + 1 - 7 = -3у² - 4у - 6.

745. а) (4 - 2х) + (5х - 3) = (х - 2) - (х + 3) ⇒ 4 - 2х + 5х - 3 = х - 2 - х - 3 ⇒ 3х = -6 ⇒ х = -2; б) 5 - 3у - (4 - 2у) = у - 8 - (у - 1) ⇒ 5 - 3у - 4 + 2у = у - 8 - у + 1 ⇒ -у = -8 ⇒ у = 8;

в) 7 -1,5а + (0,5а - 5,5) = 2а + 0,75 - (0,5 + 0,5а) ⇒ 7 - 1,5а + 0,5а - 5,5 = 2а + 0,75 - 0,5 - 5а ⇒ 2,5а = 1,25 ⇒ а = 0,5;

г) -3,6 - (1,5х + 1) = -4х - 0,8 - (0,4х - 2) ⇒ -3,6 - 1,5х - 1 = -4х - 0,8 - 0,4х + 2 ⇒ 2,9х = 5,8 ⇒ х = 2;

746. Пусть первое число 2х, тогда второе 4х, третье 5х и четвёртое 6х. Значит (5х + 6х) - (4х + 2х) = 4,8 ⇒ 11х - 6х = 4,8 ⇒ 5х = 4,8 ⇒ х = 0,96 ⇒ 2х = 1,92; 4х = 3,84; 5х = 4,8; 6х = 5,76.

747. Пусть задуманное число х. Если к задуманному числу приписать справа 0 получится 10х. Значит 143 - 10х = 3х ⇒ 13х = 143 ⇒ х = 11;

748. Пусть задуманное число х. Если к задуманному числу приписать справа 9 получится 10х + 9. Значит 10х + 9 + 2х = 633 ⇒ 12х = 624 ⇒ х = 52;

749. Пусть искомое число х. Если к трёхзначному задуманному числу приписать слева 5 получится х + 5000. Значит х + 5000 - 3032 = 9х ⇒ 8х = 1968 ⇒ x = 246;

<<< К началу