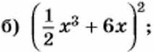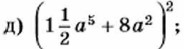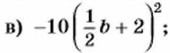|
|
|
|
|
§ 12. Квадрат суммы и квадрат разности Возведение в квадрат и в куб суммы и разности двух выражений (окончание)812. Преобразуйте в многочлен:
813. Представьте в виде многочлена:
814. Замените знак * одночленом так, чтобы получившееся равенство было тождеством: а) (* + 2b)2 = a2 + 4ab + 4b2; б) (3х + *)2 = 9х2 + 6ах + а2; в) (* - 2m)2 = 100 - 40m + 4m2; г) (* - 9с)2 = 36а4 - 108а2с + 81с2; д) (5у + *)2 = 25р2 + 4х3y + 0,16х6; е) (3а + 2,5b)2 = 9а2 + 6,25b2 + *. 815. Упростите выражение:
816. Представьте в виде многочлена:
817. Упростите выражение:
818. Упростите выражение и найдите его значение: а) (х - 10)2 — х(х + 80) при х = 0,97; б) (2х + 9)2 - х(4х + 31) при x = -16,2; в) (2x + 0,5)2 - (2х - 0,5)2 при х = -3,5; г) (0,1x - 8)2 + (0,1x + 8)2 при х = -10. 819. Решите уравнение:
820. Найдите корень уравнения:
821. Представьте в виде многочлена выражение:
822. Преобразуйте в многочлен выражение:
823. Представьте в виде многочлена:
824. Докажите тождество: а) (а + b)2 + (а - b)2 = 2(а2 + b2); б) (а + b)2 - (а - b)2 = 4ab; в) а2 + b2 = (а + b)2 - 2ab; г) (а + b)2 - 2b(а + b) = а2 - b2. 825. Докажите тождество Диофанта (111 в.): (a2 + b2) (с2 + d2) = (ас + bd)2 + (ad - bc)2. 826. При каком значении х: а) квадрат двучлена х + 1 на 120 больше квадрата двучлена х - 3; б) квадрат двучлена 2х + 10 в 4 раза больше квадрата двучлена х - 5? 827. Пользуясь формулой куба суммы, преобразуйте в многочлен выражение: а) (а + 2)3; б) (2х + у)3; в) (a + 3b)3. 828. Пользуясь формулой куба разности, преобразуйте в многочлен выражение: а) (b - 4)3; б) (1 - 2с)3; в) (2а - 3)3. 829. Упростите выражение: а) (х + 3)3 - (х - 3)3; б) (а - 2b)3 + 6ab(a - 2b). Упражнения для повторения 830. Запишите в виде выражения: а) разность квадратов 2m и 7n; б) квадрат разности х и 8у; в) утроенное произведение 6а и b2; г) произведение суммы а и b и их разности. 831. Разложите на множители многочлен а3 + 2а + а2 + 2. 832. Из пунктов А и В, расстояние между которыми 1020 км, отправились одновременно навстречу друг другу два поезда, причём скорость одного была на 10 км/ч больше скорости другого. Через 5 ч поезда, ещё не встретившись, находились на расстоянии 170 км друг от друга. Найдите скорости поездов.
|
|
|