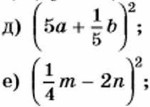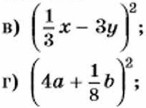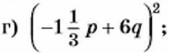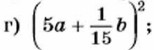|
|
|
|
|
§ 12. Квадрат суммы и квадрат разности Возведение в квадрат и в куб суммы и разности двух выражений (продолжение)Пример 5. Возведём в куб сумму 2х + 3.
(2х + 3)3 = (2х)3 + 3(2х)2 • 3 + 3 • 2х • 32 + 33 = 8х3 + 36х2 + 54х + 27. Пример 6. Возведём в куб разность 3х - б.
(3х - 5)2 = (3х)3 - 3 (3х)2 • 5 + 3 • 3 • 52 - 53 = 27х33 - 135х2 + 225х - 125.
ЕВКЛИД — древнегреческий математик, живший на рубеже IV—III вв. до н. э.. автор знаменитого трактата «Начала», посвящённого элементарной геометрии, теории чисел. Оказал огромное влияние на развитие математики. Упражнения 799. Представьте в виде многочлена:
800. Преобразуйте в многочлен:
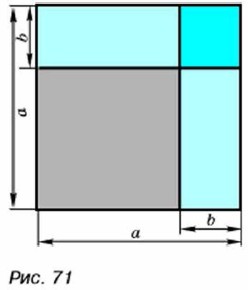
801. С помощью рисунка 71 разъясните геометрический смысл формулы (а - b)2 = а2 - 2аb + b2 для положительных а и b, удовлетворяющих условию а > b.
802. Проверьте, что равенство n2 + (n + 2)2 + (n + 9)2 = (n - 1)2 + (n + 5)2 + (n + 7)2 + 10 верно при n = 3. Покажите, что это равенство верно при любом n. 803. Преобразуйте выражение в многочлен:
804. Преобразуйте в многочлен:
805. Преобразуйте в многочлен: a) (-х + 5)2; б) (-2 - 2)2; в) (-n + 4)2; г) (-m - 10)2. 806. Из выражений (р - х)2, (у + х)2, (-у + х)2, (-х + р)2, (-х - р)2 выберите те, которые тождественно равны выражению: а) (х + у)2; б) (х - у)2. 807. Докажите тождество: а) (а - b)2 = (b - а)2; б) (-а - b)2 = (а + b)2. 808. Представьте в виде многочлена квадрат двучлена:
809. Преобразуйте в многочлен:
810. Используя формулу квадрата суммы или формулу квадрата разности, вычислите:
811. Выполните возведение в квадрат:
|
|
|



 Имеем
Имеем