|
|
|
|
Главная >> Решенния упражнений к учебнику Макарычева. Алгебра 7 класс |
|
|
Домашние работы Возведение в квадрат и в куб суммы и разности двух выражений (окончание)817. а) (x - 3)2 + x • (x + 9) = x2 - 6x + 9 + x2 + 9x = 2x2 + 3x + 9; б) (2а + 5)2 - 5 • (4а + 5) = 4а2 + 20а + 25 - 20а - 25 = 4а2; в) 9b • (b - 1) - (3b + 2)2 = 9b2 - 9b - 9b2 - 12b - 4 = -21b - 4; г) (b - 4)2 + (b - 1)(2 - b) = b2 - 8b + 16 + 2b - b2 - 2 + b = -5b + 14; д) (а + 3)(5 - а) - (а - 1)2 = 5а - а2 + 15 - 3а - а2 + 2а - 1 = -2а2 + 4а + 14; е) (5 + 2у)(у - 3) - (5 - 2у)2 = 5у - 15 + 2у2 - 6у - 25 + 20у - 4у2 = -2у2 + 19у - 40. 818. а) (х - 10) - х • (х + 80) = х2 - 20х + 100 - x2 - 80x = -100x + 100: при х = 0,97 ⇒ -100x + 100 = -100 • 0,97 + 100 = -97 + 100 = 3; б) (2х + 9)2 - х • (4х + 31) = 4х2 + 36x + 81 - 4х2 - 31x = 5x + 81: при х = -16,2 ⇒ 5x + 81 = -5 • 16,2 + 81 = -81 + 81 = 0; в) (2x + 0,5)2 - (2x - 0,5)2 = 4x2 + 2x + 0,25 - 4x2 + 2x -0,25 = 4x: при х = -3,5 ⇒ 4х - 4 • 3,5 = -14; г) (0,1х - 8)2 + (0,1x + 8)2 = 0,01x2 - 1,6x + 64 + 0,01x2 + 1,6x + 64 = 0,02x2 + 128: при х = -10 ⇒ 0,02 • (-10)2 +128 = 0,02 • 100 + 128 = 2 + 128 = 130; 819. а) (х - 6)2 - х • (x + 8) = 2 ⇒ х2 - 12x + 36 - х2 - 8х = 2 ⇒ -20x = -34 ⇒ х = 1,7; б) 9x • (х + 6) - (3x + 1) = 1 ⇒ 9x2 + 54x - 9x2 — 6x - 1 = 1 ⇒ 48x = 2 ⇒ х = в) y • (у - 1) - (у - 5)2 = 2 ⇒ у2 - у - у2 + 10у - 25 = = 2 ⇒ 9у = 27 ⇒ у = 3; г) 16у • (2 - у) + (4у - 5)2 = 0 ⇒ 32у - 16у2 + 16у2 - 40у + 25 = 0 ⇒ -8у = -25 ⇒ y = 820. а) (х - 5)2 - х2 = 3 ⇒ х2 - 10x + 25 - х2 = 3 ⇒ 10x = 22 ⇒ х = 2,2; б) (2у + 1)2 - 4у2 = 5 ⇒ 4y2 + 4у + 1 - 4у2 = 5 ⇒ 4у = 4 ⇒ у = 1; в) 9x2 - 1 - (3x - 2)2 = 0 ⇒ 9x2 - 1 - 9x2 + 12x - 4 = 0 ⇒ 12x = 5 ⇒ х = г) х + (5x + 2)2 = 25 • (1 + х2) ⇒ х + 25х2 + 20x + 4 = 25 + 25x2 ⇒ 21х = 21 ⇒ x = 1. 821. а) 7(4а - 1)2 = 7 • (16а2 - 8а + 1) = 112а2 - 56а + 7; б) -3(5у - х)2 = -3 • (25у2 - 10xу + х2) = -75у2 + 30xу - 3x2; в) -10( 822. а) 5(3а + 7)2 = 5 • (9а2 + 42а + 49) = 45а2 + 210а + 245; б) -6(4 - b)2 = -6 • (16 -8b + b2) = -96 + 48b - 6b2; в) -3(2 - х)2 - 10х = -3 • (4 - 4х + х2) - 10х = -12 + 12х - 3х2 - 10х = -12 + 2х - 3х2; г) 12а2 - 4(1 - 2а)2 + 8 = 12а2 - 4 • (1 - 4а + 4а2) + 8 = 12а2 - 4 + 16а - 16а2 + 8 = -4а2 + 16а + 4. 823. а) а(а + 9b)2 = а • (а2 +18аb + 81b2) = а3 + 18а2b + 81аb2; б) 6х(х2 + 5х)2 = 6х • (х4 + 10х3 + 25х2) = 6х5 + 60х4 + 150х3; в) (а + 2)(а - 1)2 = (а + 2)(а2 - 2а + 1) = а3 - 2а2 + а + 2а2 - 4а + 2 = а3 - 3а + 2; г) (х - 4)(х + 2)2 = (х - 4)(х2 + 4х + 4) = х3 + 4х2 + 4х - 4х2 - 16х — 16 = х3 - 12х - 16. 824. а) (а + b)2 + (а - b)2 = а2 + 2ab + b2 + а2 - 2ab + b2 - 2а2 + 2b2 = 2 • (а2 + b2); б) (а + b)2 - (а - b)2 = а2 + 2аb + b2 - а2 + 2аb - b2 = 4аb; в) (а + b)2 - 2ab - а2 + 2аb + b2 - 2аb = а2 + b2; г) (а + b)2 - 2b • (а + b) = а2 + 2аb + b2 - 2аb - 2b2 = а2 - b2. 825. (ас + bd)2 + (ad - bc)2 = а2с2 + 2abcd + b2d2 + a2d2 - 2abcd + b2c2 = (а2с2 + a2d2) + (b2c2 + b2d2) = a2 • (c2 + d2) + b2 • (с2 + d2) = (a2 + b2)(c2 + d2). 826. a) (x + 1)2 = 120 + (x - 3)2 ⇒ x2 + 2x + 1 = 120 + x2 - 6x + 9 ⇒ 8x = 128 ⇒ x = 16; б) (2x + 10)2 = 4(x - 5)2 ⇒ 4x2 + 40x + 100 = 4 • (x2 - 10x + 25) ⇒ 4x2 + 40x + 100 = 4x2 - 40x + 100 ⇒ 80x = 0 ⇒ x = 0. 827. a) (а + 2)3 = a3 + 3a2 • 2 + 3a • 22 + 8 = a3 + 6a2 + 12a + 8; 6) (2x + y)3 = 8x3 + 3 • 4 • x2y + 3 • 2xy2 + y3 = 8x3 + 12x2y + 6xy2 + у3; в) (a + 3b)3 = a3 + 3a2 • 3b + 3a • (3b)2 + 27b3 = a3 + 9a2b + 21ab2 + 27b3. 828. а) (b - 4)3 = b3 - 3b2 • 4 + 3b • 16 - 64 = b3 - 12b2 + 48b - 64; б) (1 - 2с)3 = 1 - 3 • 2с + 3 • 4с2 - 8с3 = 1 - бс + 12с2 - 8с3; в) (2а - 3)3 = 8а3 - 3 • 4а • 3 + 3 • 2а • 9 - 27 = 8а3 - 36а2 + 54а - 27. 829. а) (х + 3)3 - (х - 3)3 = х3 + 9х2 + 27х + 27 - х3 + 9х2 - 27х + 27 = 18х2 + 54; б) (а - 2b)3 + баb • (а - 2b) = а3 - 6а2b + 12аb2 - 8b3 + 6а2b - 12аb2 = а3 - 8b3. 830. а) (2m)2 - (7n)2; б) (х - 8у)2; в) 3 • (6а • b2); г) (а + b) (а - b). 831. а3 + 2а + а2 + 2 = (а3 + а2) + (2а + 2) = а2 • (а + 1) + 2 • (а + 1) = (а2 + 2)(а + 1); 832. Пусть скорость первого поезда равна υ, тогда скорость второго υ + 10. Поезда за 5 часов прошли путь 1020 - 170 = 850. Значит (υ + υ + 10) • 5 = 850 ⇒ 10υ + 50 = 850 ⇒ υ = 80 ⇒ υ + 10 = 90. Ответ: 80 км/ч и 90 км/ч.
|
|
|



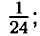
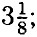
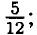
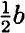 + 2)2 = -10 • (0,25b2 + 2b + 4) = -2,5b2 - 20b - 40; г) 3(а - 1)2 + 8а = 3 • (а2 - 2а + 1) + 8а = 3а2 - 6а + 3 + 8а - 3а2 + 2а + 3; д) 9с2 - 4 + 6(с - 2)2 = 9с2 - 4 + 6 • (с2 - 4с + 4) = 9c2 - 4 + 6с2 - 24с + 24 - 15с2 - 24с + 20; е) 10аb - 4(2а — b)2 + 6b2 = 10аb - 4 • (4а2 - 4аb + b2) + 6b2 = 10ab - 16а2 + 16аb - 4b2 + 6b2 = 26аb - 16а2 + 2b2.
+ 2)2 = -10 • (0,25b2 + 2b + 4) = -2,5b2 - 20b - 40; г) 3(а - 1)2 + 8а = 3 • (а2 - 2а + 1) + 8а = 3а2 - 6а + 3 + 8а - 3а2 + 2а + 3; д) 9с2 - 4 + 6(с - 2)2 = 9с2 - 4 + 6 • (с2 - 4с + 4) = 9c2 - 4 + 6с2 - 24с + 24 - 15с2 - 24с + 20; е) 10аb - 4(2а — b)2 + 6b2 = 10аb - 4 • (4а2 - 4аb + b2) + 6b2 = 10ab - 16а2 + 16аb - 4b2 + 6b2 = 26аb - 16а2 + 2b2.