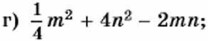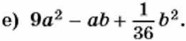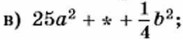Главная >> Алгебра 7 класс. Макарычев. ГДЗ

§ 12. Квадрат суммы и квадрат разности

Разложение на множители с помощью формул квадрата суммы и квадрата разности

Формулы квадрата суммы и квадрата разности находят применение не только для возведения в квадрат суммы и разности, но и для разложения на множители выражений вида а2 + 2аb + b2 и а2 - 2аb + b2.

Действительно, поменяв местами в этих формулах левую и правую части, получим

    а2 + 2аb + b2 = (а + b)2; а2 - 2аЬ + b2 = (а - b)2.

Приведённые равенства показывают, что трёхчлен а2 + 2аb + b2 можно представить в виде произведения (а + b)(а + b), а трёхчлен а2 - 2ab + b2 можно представить в виде произведений (а - b)(а - b).

Пример 1. Представим трёхчлен 9х2 + 30х + 25 в виде квадрата двучлена.

Первое слагаемое представляет собой квадрат выражения Зх, третье — квадрат числа 5. Так как второе слагаемое равно удвоенному произведению Зх и 5, то этот трёхчлен можно представить в виде квадрата суммы 3х и 5:

    9х2 + 30х + 25 = (3х)2 + 2 • 3х • 5 + 52 = (3х + 5)2.

Пример 2. Разложим на множители трёхчлен а2 - 20ab2 + 100b4.

Здесь можно применить формулу квадрата разности:

    а2 - 20ab2 + 100b4 = а2 - 2 • а • 10b2 + (10b2)2 = (а - 10b2)2 = (а - 10b2)(a - 10b2).

Упражнения

а) х2 + 2ху + у2;

б) р2 - 2pq + q2;

в) а2 + 12а + 36;

г) 64 + 16b + b2;

д) 1 - 2z + z2;

е) n2 + n4 + 4.

834. Представьте трёхчлен в виде произведения двух одинаковых множителей:

а) 4х2 + 12х + 9;

б) 25b2 + 10b + 1;

в) 9х2 - 24ху + 16у2;

д) 10ху + 0,25х2 + 100у2;

835. Преобразуйте трёхчлен в квадрат двучлена:

а) 81а2 - 18ab + b;

б) 1 + у2 - 2у;

в) 8ab + b2 + 16a2;

г) 100х2 + р2 + 20ху;

д) b2 + 4a2 - 4ab;

е) 28ху + 49х2 + 4у2.

836. Поставьте вместо знака * такой одночлен, чтобы трёхчлен можно было представить в виде квадрата двучлена:

а) * + 56а + 49;

б) 36 - 12х + *;

г) 0,01b2 + * + 100с2.

837. Впишите вместо знака * недостающие одночлены так, чтобы получилось тождество:

    а) (* + 2а)2 = * + 12ab + *; б) (3х + *)2 = * + * + 49y2.

838. Замените знак * таким одночленом, чтобы полученное выражение можно было представить в виде квадрата двучлена:

а) b2 + 20b + *;

б) * + 14b + 49;

в) 16х2 + 24ху + *;

г) * - 42pq + 49q2.

839. Представьте трёхчлен в виде квадрата двучлена или в виде выражения, противоположного квадрату двучлена:

а) -1 + 4а - 4а2;

б) -42а + 9а2 + 49;

в) 24ab - 16а2 - 9b2;

г) -44ах + 121а2 + 4х2;

д) 4cd - 25с2 - 0,16d2;

е) -0,49х2 - 1,4ху - у2.

840. Найдите значение выражения:

    а) у2 - 2у + 1 при у = 101; -11; 0,6;

    б) 4х2 - 20х + 25 при х = 12,5; 0; -2;

    в) 25а2 + 49 + 70а при а = 0,4; -2; -1,6.

841. Верно ли, что при любых значениях х:

    а) х2 + 10 > 0; б) х2 + 20х + 100 > 0?

Окончание >>>

 

 

???????@Mail.ru