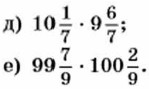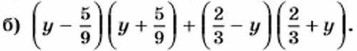К параграфу 13

971. Вычислите:

а) 1005 • 995;
б) 108 • 92;
в) 0,94 • 1,06;

г) 1,09 • 0,91;

972. Представьте в виде многочлена:

а) 5у (у² - 3)(у² + 3);

б) -8х(4х - х³)(4х + x³);

в) (а⁴ - 3)(а⁴ + 3)(а⁸ + 9);

г) (1 - b³)(1 + b³)(1 + b⁶).

973. Упростите выражение:

а) (а + 2)(а - 2) - а (а - 5);

б) (а - 3)(3 + а) + а (7 - а);

в) (b - 4)(b + 4) - (b - 3)(b + 5);

г) (b + 8)(b - 6) - (b - 7)(b + 7);

д) (с - 1)(с + 1) + (с - 9)(с + 9);

е) (5 + с)(с - 5) - (с - 10)(с + 10).

974. Докажите, что значение выражения не зависит от значения переменной:

а) (х - 8)(х + 8) - (х - 12)(x + 12);

975. Преобразуйте в многочлен:

а) (х - 5)² + 2х(х - 3);

б) (у + 8)² - 4y(y - 2);

в) (a - 4)(а + 4) + (2а - 1)²;

г) (b - 3)(b + 3) - (b + 2)²;

д) (2а -5)² - (5а - 2)²;

е) (3b - 1)² + (1 - 3b)²;

ж) (2х + 1)² - (х + 7)(х - 3);

з) (3у -2)² - (y - 9)(9 - y).

976. При каком значении х удвоенное произведение двучленов х + 2 и х - 2 меньше суммы их квадратов на 16?

977. Представьте в виде многочлена:

а) (х + у + 1)(х + у - 1);

б) (m + n - 3)(m + n + 3);

в) (а - b - 5)(а - b + 5);

г) (с - d + 8)(с - d - 8);

д) (р + 2q - 3)(р - 2q - 3);

е) (а - 3х + 6)(а + 3х + 6).

978. Решите уравнение:

а) (х - 7)² + 3 = (х - 2)(х + 2);

б) (х + 6)² - (х - 5)(х + 5) = 79;

в) (2х - 3)² - (7 - 2х)² = 2;

г) (5х - 1)² - (1 - 3х)² = 16х(х - 3).