График линейного уравнения с двумя переменными

Каждая пара чисел, являющаяся решением уравнения с переменными х и у, изображается в координатной плоскости точкой, координатами которой служит пта пара чисел (абсциссой служит значение х, а ординатой — значение у). Все такие точки образуют график уравнения.

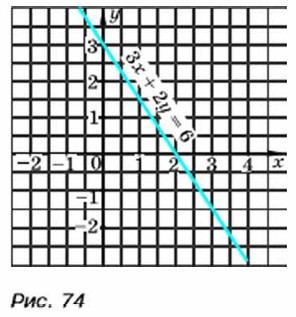
Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения.

Выясним, что представляет собой график уравнения

3х + 2у = 6.

Выразим переменную у через х:

у = -1,5x + 3.

Формулой у = - 1,5х + 3 задаётся линейная функция, графиком которой служит прямая (рис. 74). Так как уравнения

3х + 2у = 6 и у = -1,5x + 3

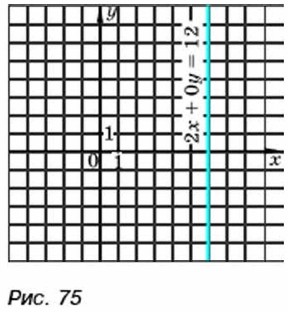
равносильны, то эта прямая является и графиком уравнения 3х + 2у = 6.

С помощью таких же рассуждений можно показать, что графиком любого линейного уравнения с переменными х и y, в котором коэффициент при у не равен нулю, является прямая.

Если в линейном уравнении коэффициент при у равен нулю, а коэффициент при х отличен от нуля, то графиком такого уравнения также является прямая.

Рассмотрим, например, уравнение

2х + 0у = 12.

Его решениями служат пары чисел (х; у), в которых х = 6, а у — любое число, например (6; 2), (6; 0), (6; -4,5). График уравнения состоит из всех точек, абсцисса которых равна 6, а ордината — произвольному числу. Такие точки образуют прямую, проходящую через точку (6; 0) и параллельную оси у (рис. 75).

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен пулю, является прямая.

Рассмотрим теперь случай, когда в линейном уравнении оба коэффициента при переменных равны нулю.

Уравнение

ах + by = с,

в котором оба коэффициента при переменных равны нулю, имеет вид 0х + 0у = с. При с = 0 любая пара чисел является решением этого уравнения, а его графиком — вся координатная плоскость. При с ≠ 0 уравнение не имеет решений и его график не содержит ни одной точки.

Окончание >>>