|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений Линейное уравнение с двумя переменным1025. Линейным уравнением с двумя переменными называется уравнение вида ах + by = с, где х и у — переменные, а, b и с — некоторые числа: а) 3х — у = 17 — уравнение является линейным; б) х2 - 2у = 5 — уравнение не является линейным; в) 13х + 6y = 0 — уравнение является линейным; г) ху + 2х = 9 — уравнение не является линейным. 1026. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство. Дано: х + у = 6. При х = 1027. а) пары значений переменных x и у (-4; 3), (-1; -3), (0; -5) — являются решением уравнения 2х + у = -5; б) пары значений переменных х и у: (-5; 0), (4; -3) — являются решением уравнения х + 3у - 5. 1028. Решением уравнения 10х + у = 10 являются пары чисел (0,1; 11), (1; 2). 1029. а) х = 2, у = 4,5; х + у = 6,5; б) х = -1, у = 2; х + у = 1. 1030. а) 4х - 3у = 12 ⇒ 3у = 4х - 12 ⇒ у = 1031. а) 2u + υ = 4 ⇒ υ = 4 - 2u; б) 2u + υ = 4 ⇒ 2u = 4 — υ ⇒ u = 2 - 0,5υ. 1032. а) 3x + 2у = 12 ⇒ 2у = 12 - 3x ⇒ у = 6 - 1,5x; (2; 3);(4; 0); (0; 6); б) 5у - 2х = 1 ⇒ 5у = 1 + 2x ⇒ у = 0,2 + 0,4x: (0; 0,2); (1; 0,6); (2; 1). 1033. а) x - 6у = 4; х = 6у + 4. Решением данного уравнения являются пары чисел (10; 1); (4; 0); (-2; -1); б) 3x - у = 10; у = 3x - 10; Решением данного уравнения являются пары чисел (0; -10); (1; -7); 1034. Необходимо среди решений уравнения а + 2у = 18 найти пару составленную из двух одинаковых чисел, то есть х - у; x + 2x = 18; 3x = 18; х - 6; у = 6. Искомая пара чисел (6; 6). 1035. Пара х = 2, у = 1 является решением уравнения аx + 2у = 8; значит а • 2 + 2 • 1 = 8 ⇒ 2а + 6 ⇒ а = 3. 1036. Пусть двухрублевых монет было х, а пятирублевых у. Тогда 2x + 5у = 28 ⇒ x = 1037. Пусть ученик купил х тетрадей и у карандашей. Тогда 5x + 7у = 44 ⇒ у = 1038. Пусть хозяйка купила мелких тарелок х глубоких y. Тогда 30x + 35у = 320 ⇒ 35у = 320 - 30x ⇒ у = 1039. Пусть количество пакетов по 3 кг х, а по 2 кг у. Значит 3x + 2у = 20 ⇒ у = 10 - 1,5x; Значит х чётное: при х = 2 ⇒ у = 7; при х = 4 ⇒ у = 4; при x = 6 ⇒ у = 1. 1040. Пусть всего тетрадей в клетку купили а;, а в линейку у, х и у целые числа больше нуля. Тогда 15x + 10у = 320 ⇒ у = 32 - 1,5x: а) при х = у ⇒ 25x = 320 ⇒ х = 12,8; одинаковое количество тетрадей невозможно купить; б) все возможные пары: (2; 29); (4; 26); (6; 23); (8; 20); (10; 17); (12; 14); (14; 11); (16; 8); (18; 5); (20; 2); в) максимальное количество тетрадей при х = 2 ⇒ у = 29 ⇒ х + у = 31; г) минимальное количество тетрадей при х = 20 ⇒ у = 2 ⇒ х + у = 22. 1041. Пусть первоначально было число 1042. х — искомое число: х = 5q + 1 ⇒ х = 6ω + 2 ⇒ 5q + 1 = 6ω + 2 ⇒ q = 1043. а) 2с(с - 4)2 - с2 • (2с -10) = 2с • (с2 - 8с + 16) - 2с3 + 10с2 = 2с3 - 16с2 + 32с - 2с3 + 10с2 = -6с2 + 32с = с • (32 - 6с): при с = 0,2 ⇒ с • (32 - 6с) = 0,2 • (32 - 1,2) = 6,16; б) (а - 4b)(4b + а) = а2 - 16b2: при а = 1,2 и b = -0,6 ⇒ а2 - 16b2 = 1,44 - 16 • 0,36 = -4,32; в) 3Z2 — 0,6р2 = 3р + 0,6р2 + 0,03р3 - 0,6p2 = 3 • (р + 0,03р3): при р = -2 ⇒ 3 • (р + 0,03р3) = 3 • (-2 - 0,24) = -6,72. 1044. а) 1 + а - а2 - а3 = (1 + а) - а2 • (1 + а) - (1 - а2)(1 + а) = (1 - а)(1 + а)(1 + а); б) 8 - b3 + 4b - 2b2 = 4 • (2 + b) - b2 • (b + 2) = (4 - b2)(b + 2) = (2 - b)(2 + b)(b + 2).
|
|
|



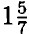 и у =
и у = 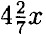 + у =
+ у = 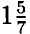 +
+ 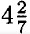 = 6; пара чисел является решением данного уравнения. х = 6, у = 0 и х = 0, у = 6; — так же являются решением данного уравнения.
= 6; пара чисел является решением данного уравнения. х = 6, у = 0 и х = 0, у = 6; — так же являются решением данного уравнения.
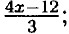 б) 4x - 3у = 12 4x = 12 + 3у ⇒ x =
б) 4x - 3у = 12 4x = 12 + 3у ⇒ x = 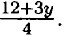
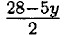 = 14 -
= 14 - 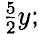 так как количество монет должно быть целым числом то у обязательно чётное число: при у = 0; х = 14 - 2,5у = 14; при у = 2; x = 14 - 5 = 9; при у = 4; x = 14 - 10 = 4. Ответ: было взято 9, или 4.
так как количество монет должно быть целым числом то у обязательно чётное число: при у = 0; х = 14 - 2,5у = 14; при у = 2; x = 14 - 5 = 9; при у = 4; x = 14 - 10 = 4. Ответ: было взято 9, или 4.
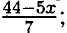 х и у должны быть целыми и больше нуля: x = 6, у = 2.
х и у должны быть целыми и больше нуля: x = 6, у = 2.
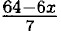 ⇒ х = 6, у = 4;
⇒ х = 6, у = 4;
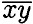 . Тогда
. Тогда 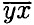 - 54 ⇒ 10x + у = 10у + x - 54 ⇒ 9x = 9у - 54 ⇒ х = у - 6. При у = 7x = 1; у = 8, х = 2; у = 9x= 3. Ответ: 17. 28 и 39.
- 54 ⇒ 10x + у = 10у + x - 54 ⇒ 9x = 9у - 54 ⇒ х = у - 6. При у = 7x = 1; у = 8, х = 2; у = 9x= 3. Ответ: 17. 28 и 39.
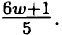 Минимальное целое w которое удовлетворяет равенству 4: х = 6ω + 2 = 26. Ответ: 26.
Минимальное целое w которое удовлетворяет равенству 4: х = 6ω + 2 = 26. Ответ: 26.