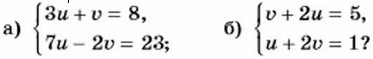|
|
|
|
|
§ 15. Линейные уравнения с двумя переменными и их системы Системы линейных уравнений с двумя переменными (продолжение)Рассмотрим системы двух линейных уравнений с двумя переменными, в каждом из которых хотя бы один из коэффициентов при переменных отличен от нуля. Выясним, всегда ли такая система имеет решения и если имеет, то сколько. Графиками уравнений системы являются прямые. Если эти прямые пересекаются, то система имеет единственное решение; если прямые параллельны, то система не имеет решений; если прямые совпадают, то решений бесконечно много. Пример 1. Выясним, сколько решений имеет система уравнений
Уравнениями у = -1,1x + 12 и у = -6x + 18 задаются линейные функции. Угловые коэффициенты прямых, являющихся графиками этих функций, различны. Значит, эти прямые пересекаются и система имеет единственное решение. Пример 2. Рассмотрим, сколько решений имеет система уравнений
Прямые, являющиеся графиками линейных функций у = -0,4x + 0,15 и у = -0,4x + 3,2, параллельны, так как их угловые коэффициенты одинаковы, а точки пересечения с осью у различны. Отсюда следует, что данная система уравнений не имеет решений. Пример 3. Выясним, сколько решений имеет система уравнений
Очевидно, что графики уравнений совпадают. Это означает, что любая пара чисел (x0; y0), в которой x0 — произвольное число, а у0 = -2,5x0 - 9, является решением системы. Система имеет бесконечно много решений. Упражнения 1056. Является ли решением системы уравнений а) x = 3, у - 1; б) x = 2, у = 2? 1057. Является ли пара чисел u = 3, υ = - 1 решением системы уравнений:
|
|
|



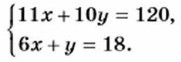
 Рассмотрим, каково взаимное расположение графиков уравнений данной системы. Для этого выразим из каждого уравнения у через *, получим
Рассмотрим, каково взаимное расположение графиков уравнений данной системы. Для этого выразим из каждого уравнения у через *, получим
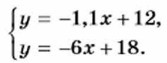

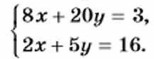
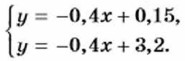
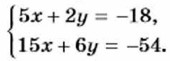
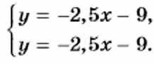
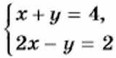 пара чисел:
пара чисел: