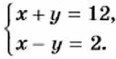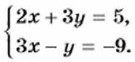Системы линейных уравнений с двумя переменными

Задача. Сумма двух чисел равна 12, а их разность равна 2. Найдите эти числа.

Обозначим первое число буквой х, а второе буквой у. По условию задачи сумма чисел равна 12, т. е.

х + у = 12.

Так как разность чисел равна 2, то

х - у = 2.

Мы составили два уравнения с двумя переменными. Чтобы ответить на вопрос задачи, надо найти такие значения переменных, которые обращают в верное равенство каждое из уравнений х + у = 12 и х - у = 2, т. е. найти общие решения этих уравнений. В таких случаях говорят, что требуется решить систему уравнений.

Систему уравнений принято записывать с помощью фигурной скобки. Составленную систему уравнений можно записать так:

Пара значений переменных х = 7, у = 5 служит решением каждого уравнения системы, так как оба равенства 7 + 5=12 и 7 - 5 = 2 являются верными. Такую пару называют решением системы.

Определение. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.

Решить систему уравнений — значит найти все её решения или доказать, что решений нет.

Для того чтобы решить систему линейных уравнений с двумя переменными, можно использовать графики уравнений.

Пусть требуется решить систему уравнений

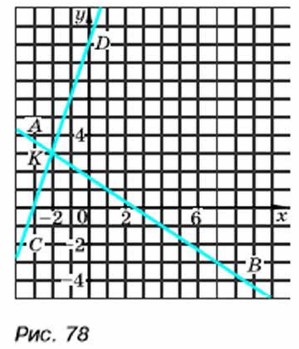
Построим в координатной плоскости графики уравнений системы. Графиком первого уравнения является прямая АВ, а графиком второго — прямая CD (рис. 78).

Координаты любой точки прямой AВ являются решением уравнения 2х + 3у = 5, а координаты любой точки прямой CD являются решением уравнения 3х - у = -9. Координаты точки пересечения прямых удовлетворяют как первому уравнению, так и второму, т. о. являются решением системы. Графики пересекаются в точке К(-2; 3). Значит, система имеет единственное решение: х = -2, у = 3.

Применённый нами способ решения системы уравнений называется графическим. Заметим, что графический способ обычно позволяет находить решения лишь приближённо.

Продолжение >>>