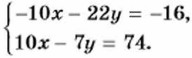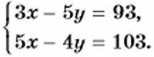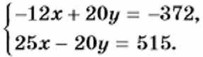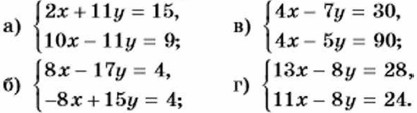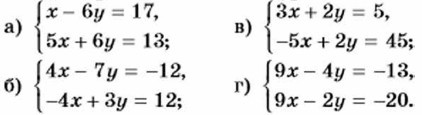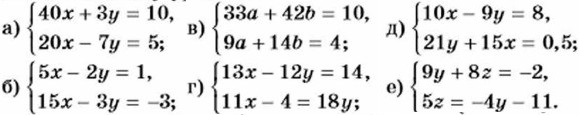|
|
|
|
|
§ 16. Решение систем линейных уравнений Способ сложения (продолжение)Пример 2. Решим систему уравнений
Теперь почленное сложение приводит к уравнению с одной переменной -29у = 58. Из этого уравнения находим, что у = -2. Подставив во второе уравнение вместо у число -2, найдём значение х: 10x - 7 • (-2) = 74, 10x = 60, x = 6. Ответ. x = 6, у = -2. Пример 3. Решим систему уравнении
Отсюда найдём, что 13x = 143, x = 11. Подставив значение * в уравнение 5x - 4у = 103, найдём, что у = -12. Ответ. x = 11, у = -12. Мы рассмотрели примеры решения систем способом сложения. При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
Заметим, что если коэффициенты при одной из переменных являются противоположными числами, то решение сразу начинают с почленного сложения уравнений. Упражнения 1082. Решите систему уравнений:
1083. Найдите решение системы уравнений:
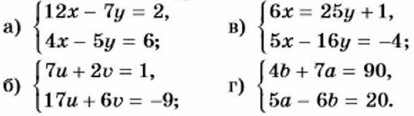
1084. Решите систему уравнений:
1085. Решите систему уравнений:
|
|
|



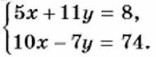
 Почленное сложение уравнений системы не приведёт к исключению одной из переменных. Однако если умножить все члены первого уравнения на -2, а второе уравнение оставить без изменений, то коэффициенты при х в полученных уравнениях будут противоположными числами:
Почленное сложение уравнений системы не приведёт к исключению одной из переменных. Однако если умножить все члены первого уравнения на -2, а второе уравнение оставить без изменений, то коэффициенты при х в полученных уравнениях будут противоположными числами: