Способ сложения

Рассмотрим ещё один способ решения систем линейных уравнений — способ сложения. При решении систем отим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Пример 1. Решим систему уравнений

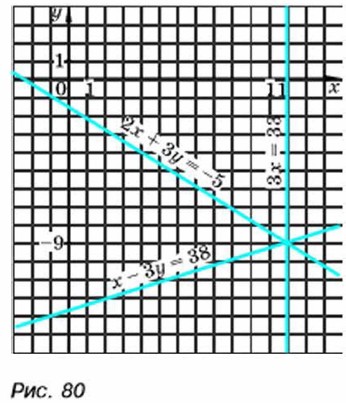
В уравнениях этой системы коэффициенты при у являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной Зх = 33. Заменим одно из уравнений системы (1), например первое, уравнением Зх = 33. Получим систему

Система (2) равносильна системе (1).

Решим систему (2). Из уравнения 3х = 33 находим, что х= 11.

Подставив это значение х в уравнение

х - 3у - 38,

получим уравнение с переменной у:

11 - 3у = 38.

Решим это уравнение:

-3у = 27,

y = -9.

Пара (11; -9) — решение системы (2), а значит, и данной системы (1).

Воспользовавшись тем, что в уравнениях системы (1) коэффициенты при у являются противоположными числами, мы свели её решение к решению равносильной системы (2), в которой одно из уравнений содержит только одну переменную.

Геометрически равносильность систем (1) и (2) означает, что графики уравнений 2x + 3у = -5 и х - 3у = 38 пересекаются в той же точке, что и графики уравнений 3x = 33 и х - 3у = 38, т. е. все три прямые пересекаются в одной точке (рис. 80).

Продолжение >>>