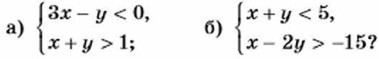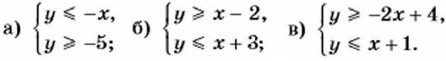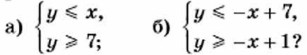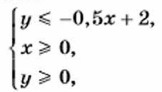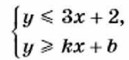|
|
|
|
|
§ 16. Решение систем линейных уравнений Линейные неравенства с двумя переменными и их системы (окончание)Пример 2. Выясним, какое множество точек задаёт на координатной плоскости система неравенств
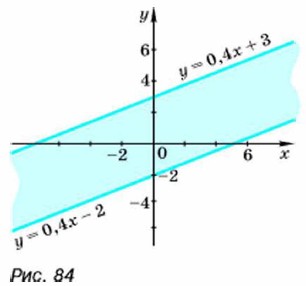
у = 0,4x - 2 и у = 0,4x + 3. Так как угловые коэффициенты прямых равны, то эти прямые параллельны. Первое нестрогое неравенство задаёт прямую у = 0,4x - 2 и полуплоскость, расположенную выше этой прямой, а второе — прямую у = 0,4x + 3 и полуплоскость, расположенную ниже этой прямой. Рассматриваемая система неравенств задаёт общую часть этих множеств.
Эта общая часть представляет собой полосу, ограниченную прямыми у = 0,4x - 2 и у = 0,4x + 3 (рис. 84). Упражнения 1128. Постройте прямую
1129. Покажите штриховкой множество точек координатной плоскости, которое задаёт неравенство: а) у ≥ х; б) у ≤ -x; в) x ≥ 1; г) у ≤ 5. 1130. Изобразите множество точек, которое задаёт на координатной плоскости неравенство: а) у ≥ х + 1; б) у < - 0,2x + 3. 1131. Задайте неравенством полуплоскость, расположенную выше прямой: а) у = х - 1,3; б) x + у = 5. 1132. Является ли пара чисел x = -3, у = 4 решением системы неравенств:
1133. Изобразите на координатной плоскости множество точек, которое задаёт система неравенств:
1134. Какую фигуру на координатной плоскости задаёт система неравенств:
1135. Изобразите на координатной плоскости фигуру, которую задаёт система неравенств
и найдите её площадь. 1136. Укажите какие-либо значения k и b, при которых система неравенств
задаёт на координатной плоскости: а) полосу; б) угол.
|
|
|



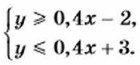
 Построим в координатной плоскости прямые, являющиеся графиками уравнений
Построим в координатной плоскости прямые, являющиеся графиками уравнений

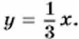 Покажите штриховкой множество точек координатной плоскости, координаты которых удовлетворяют неравенству:
Покажите штриховкой множество точек координатной плоскости, координаты которых удовлетворяют неравенству: