Линейные неравенства с двумя переменными и их системы

Неравенство у > 0,5х + 2 при х = 6, у = 10 обращается в верное неравенство 10 > 0,5 • 6 + 2. Говорят, что пара значений переменных х = 6, у = 10 является решением этого неравенства.

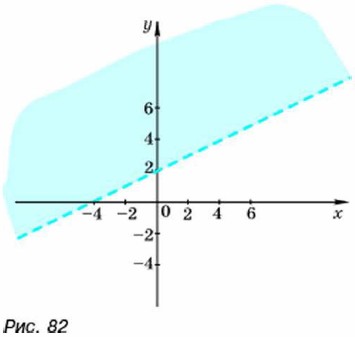
Определение. Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное числовое неравенство.

Нетрудно проверить, что решениями неравенства

у > 0,5х + 2

являются также пары х = 0, у = 5; х = -8, у = -1. Каждое решение неравенства у > 0,5х + 2 можно изобразить точкой на координатной плоскости.

Выясним, какое множество точек задаёт на координатной плоскости рассматриваемое неравенство.

Множество точек, координаты которых удовлетворяют уравнению у = 0,5х + 2, представляет собой прямую (рис. 82). Если точка плоскости лежит выше, чем точка этой прямой, находящаяся с ней на одной вертикали (см. рис. 82), то её ордината больше ординаты соответствующей точки прямой и потому координаты этой точки удовлетворяют неравенству у > 0,5х + 2.

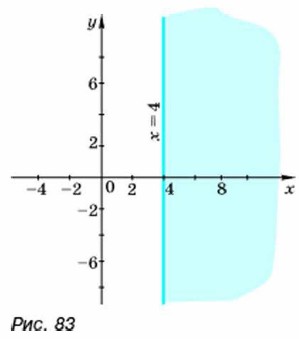
Вообще координаты любой точки полуплоскости, расположенной выше прямой у = 0,5х + 2, удовлетворяют неравенству у > 0,5х + 2, а координаты других точек плоскости этому неравенству не удовлетворяют.

Таким образом, неравенство у > 0,5х + 2 задаёт полуплоскость, расположенную выше прямой у = 0,5х + 2. На рисунке 82 эта полуплоскость показана цветом. Граничная прямая, не принадлежащая этой полуплоскости, проведена пунктиром.

Пример 1. Покажем в координатной плоскости множество точек, которое задаёт неравенство х ≥ 4.

Проведём прямую х = 4 (рис. 8,3).

Абсцисса любой точки, принадлежащей этой прямой или расположенной правее её, равна 4 или больше 4. Значит, неравенство х ≥ 4 задаёт на координатной плоскости прямую х = 4 и полуплоскость, расположенную правее прямой х = 4. Эта полуплоскость показана на рисунке цветом. Граничная прямая принадлежит этой полуплоскости.

Окончание >>>