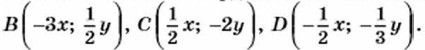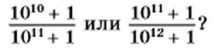|
|
|
|
|
Алгебра 7 класс Задачи повышенной трудности (продолжение)1184. Найдите все натуральные значения а, при которых корень уравнения (а - 1)x = 12 является натуральным числом. 1185. Решите уравнение:
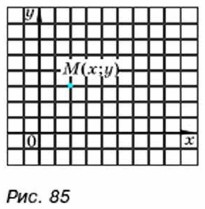
1186. В шестизначном числе первая цифра совпадает с четвёртой, вторая — с пятой и третья — с шестой. Докажите, что это число кратно 7, 11, 13. 1187. В двух бочках было воды поровну. Количество воды в первой бочке сначала уменьшилось на 10%, затем увеличилось на 10%, а во второй бочке сначала увеличилось на 10%, а затем уменьшилось на 10%. В какой бочке стало больше воды? 1188. Свежие грибы содержат 90% воды, а сухие грибы — 12% воды. Сколько получится сухих грибов из 11 кг свежих? 1189. Три ящика наполнены орехами. Во втором ящике на 10% орехов больше, чем в нервом, и на 30% больше, чем в третьем. Сколько орехов в каждом ящике, если в первом на 80 орехов больше, чем в третьем? 1190. Докажите, что сумма 13 + 23 + ... + 993 делится на 100. 1191. Число а составляет 80% числа b, а число с составляет 140% числа b. Найдите числа а, b и с, если число с больше а на 72. 1192. Число а составляет 75% числа b и 40% числа с. Число с на 42 больше числа b. Найдите числа а и b. 1193. Какое двузначное число в 4 раза больше суммы его цифр? 1194. Делится ли число 1195. Докажите, что остаток от деления простого числа на 30 есть простое число или единица. 1196. К некоторому двузначному числу слева и справа приписали по единице. В результате получили число, в 23 раза большее первоначального. Найдите это двузначное число. 1197. В двузначном числе зачеркнули одну цифру. Получилось число, которое в 31 раз меньше первоначального. Какую цифру и в каком числе зачеркнули? 1198. Первая цифра трёхзначного числа 8. Если эту цифру переставить на последнее место, то число увеличится на 18. Найдите первоначальное число. 1199. Постройте график уравнения: а) (х - 2) (у + 3) = 0; б) х2 + ху = 0. 1200. Постройте график уравнения: а) у + |у| = х; б) у = х|у|. 1201. Постройте график функции: а) у = |х| - 3; б) у = 4 - |х|. 1202. Найдите наименьшее натуральное число, которое после умножения на 2 станет квадратом, а после умножения на 3 — кубом натурального числа. 1203. Докажите, что значение выражения 967 - 225 - 486 кратно 10. 1204. В координатной плоскости (рис. 85) отмечена точка М(х; у). Отметьте в этой координатной плоскости точки A(2х;2у),
1205. Что больше:
1206. Представьте выражение 2х2 + 2у2 в виде суммы двух квадратов. 1207. Если х ≠ 0 или у ≠ 0, то значение выражения 15х2 - 18xy + 15у2 положительно. Докажите это.
|
|
|



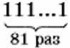 на 81?
на 81?