|
|
|
|
|
Алгебра 7 класс Задачи повышенной трудности (окончание)1208. Разложите на множители многочлен: а) х8 + х4 - 2; б) а5 - а2 - а - 1; в) n4 + 4; г) n4 + n2 + 1. 1209. Докажите, что р2 - 1 кратно 24, если р — простое число, большее 3. 1210. Докажите, что разность между кубами двух последовательных натуральных чисел при делении на 6 даёт остаток 1. 1211. Докажите, что сумма квадратов пяти последовательных натуральных чисел не может быть квадратом натурального числа. 1212. Докажите, что разность между квадратом натурального числа, не кратного 3, и числом 1 кратна 3. 1213. Упростите выражение (2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)(232 + 1). 1214. Докажите, что уравнение х2 - у2 = 30 не имеет целых решений 1215. Докажите, что не существует целых коэффициентов а, b, с и d, таких, что значение многочлена ах3 + bх2 + сх + d равно 1 при х = 19 и равно 2 при х = 62. 1216. Докажите, что если у есть среднее арифметическое х и z, то х4 + 2x3z - 2xz3 - z4 - 4х2у2 + 4y2z2 = 0. 1217. Найдите все простые числа р и qy для которых р2 - 2q2 = 1. 1218. При каких значениях а, b, с и d является тождеством равенство bх3 - 32х2 + 75х - 71 = а(х - 2)3 + b(x - 2)2 + с(х - 2) + d? 1219. Представьте многочлен 3х3 + 7х2 + 9х + 6 в виде многочлена ay3 + by2 + су + d, где у = х + 1. 1220. При каких натуральных значениях х и у верно равенство 3х + 7 у = 23? 1221. Решите систему уравнений:
1222. Найдите трёхзначное число, которое равно квадрату двузначного числа и кубу однозначного числа. 1223. Найдите два натуральных числа, сумма которых равна 168, а их наибольший общий делитель равен 24. 1224. Найдите все пары простых чисел, которые являются решениями уравнения х + у = 26. 1225. Путь от А до В идёт 3 км в гору, 6 км иод гору и 12 км но ровному месту. Этот путь мотоциклист проделал за 1 ч 7 мин, а обратный путь — за 1 ч 16 мин. Найдите скорость мотоциклиста в гору и под гору, если на ровном месте его скорость 18 км/ч. 1226. Задача Л. Н. Толстого. Вышла в ноле артель косцов. Ей предстояло скосить два луга, из которых один был вдвое больше другого. Полдня вся артель косила большой луг, а на вторую половину дня артель разделилась пополам, и одна половина осталась докашивать большой луг, а другая стала косить малый луг. К вечеру большой луг был скошен, а от малого остался участок, который был скошен на другой день одним косцом, работавшим весь день. Сколько было косцов в артели? 1227. Из двух городов Ли В, расстояние между которыми 180 км, в 6 ч 20 мин вышли навстречу друг другу автобус и легковой автомобиль. Их встреча произошла в 7 ч 50 мин. Если бы автобус вышел на 1 ч 15 мин раньше, а легковой автомобиль на 15 мин позже, то они встретились бы в 7 ч 35 мин. Какова скорость автобуса и легкового автомобиля? 1228. Из города А в город В в 8 ч 50 мин вышли два автобуса. В то же в(юмя из города В в город А выехал велосипедист. Один автобус он встретил в 10 ч 10 мин, а другой — в 10 ч 50 мин. Расстояние между городами 100 км. Найдите скорость велосипедиста, если скорость одного автобуса в 1229. Всадник и пешеход одновременно отправились из пункта А в пункт В. Всадник, прибыв в пункт В на 50 мин раньше пешехода, возвратился обратно в пункт А. На обратном пути он встретился с пешеходом в двух километрах от пункта В. На весь путь всадник затратил 1 ч 40 мин. Найдите расстояние от Л до В и скорость всадника и пешехода. 1230. Только что добытый каменный уголь содержит 2% воды, а после двухнедельного пребывания на воздухе он содержит 12% воды. На сколько килограммов увеличилась масса добытой тонны угля после того, как уголь две недели был на воздухе? 1231. Два брата ходят из школы домой с одинаковой скоростью. Однажды через 15 мин после выхода из школы первый побежал в школу и, добежав до неё, немедленно бросился догонять второго. Оставшись один, второй продолжал идти домой в 2 раза медленнее. Когда первый брат догнал второго, они пошли с первоначальной скоростью и пришли домой на 6 мин позже, чем обычно. Во сколько раз скорость бега первого брата больше обычной скорости ходьбы братьев?
|
|
|



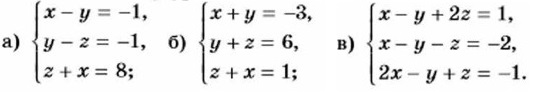
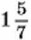 раза больше скорости другого.
раза больше скорости другого.