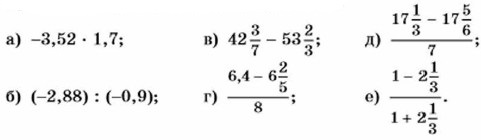Решение задач с помощью уравнений (окончание)

158. Для ремонта школы прибыла бригада, в которой было в 2,5 раза больше маляров, чем плотников. Вскоре прораб включил в бригаду ещё четырёх маляров, а двух плотников перевёл на другой объект. В результате маляров в бригаде оказалось в 4 раза больше, чем плотников. Сколько маляров и сколько плотников было в бригаде первоначально?

159. (Для работы в парах.) В классе учится ... учащихся. Отношение числа девочек к числу мальчиков равно 5 : 4. Сколько девочек и сколько мальчиков учится в классе?

1) Выясните, какие числа, соответствующие смыслу задачи, можно поставить вместо многоточия.

2) Предложите друг другу закончить решение для одного из найденных чисел.

3) Обсудите полученные ответы.

160. В корзине было в 2 раза меньше винограда, чем в ящике. После того как в корзину добавили 2 кг, в ней стало винограда на 0,5 кг больше, чем в ящике. Сколько винограда было в корзине?

161. Один арбуз на 2 кг легче, чем другой, и в 5 раз легче, чем третий. Первый и третий арбузы вместе в 3 раза тяжелее, чем второй. Найдите массу каждого арбуза.

162. В двух мешках было но 50 кг сахара. После тот как из одного мешка взяли в 3 раза больше сахара, чем из другого, в нём осталось в 2 раза меньше сахара, чем в другом. Сколько сахара осталось в каждом мешке?

Упражнения для повторения

163. Постройте в координатной плоскости точку, у которой:

а) абсцисса равна 3, а ордината противоположна абсциссе;

б) абсцисса равна -2, а ордината на единицу больше;

в) абсцисса равна 1,5, а ордината на единицу меньше;

г) абсцисса равна 6, а ордината — противоположному числу.

164. Постройте в координатной плоскости отрезок MN, зная координаты его концов: М (-1; 4) и N(2; -2). Найдите координаты точек пересечения этого отрезка с осью х и с осью у.

165. Найдите значение выражения -0,5(7b - 12а) - (8,4а - 14b) при а = -10, b = -6.

166. Сравните с нулём значение выражения:

Контрольные вопросы и задания

1. Сформулируйте определение корня уравнения. Является ли число 7 корнем уравнения: 6х = 42; 0х = 11; (16 - 2 • 8)х = 0?

2. Что значит решить уравнение? Решите уравнение: 6x = -12; х - 2х • 6 = 0; 5х - 4х = 6 + х.

3. Какие уравнения называются равносильными? Сформулируйте свойства уравнений. Приведите пример уравнения, равносильного уравнению: 5х - 1 = 3; 0,2x = 1,1; 3х - 4х + 6 = 0.

4. Дайте определение линейного уравнения с одной переменной. Приведите примеры.

5. В каком случае уравнение ах = b имеет единственный корень; имеет бесконечно много корней; не имеет корней? Приведите примеры.

<<< К началу Решенния >>>