|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Домашние работы Решение задач с помощью уравнений143. Пусть в первой кассе продали х билетов, тогда во второй продали х + 36. Тога в первой и второй продали х + х + 36 = 2х + 36 билетов. Значит 2х + 36 = 392 ⇒ 2х — 356 ⇒ х = 178 — продали билетов в первой кассе, х + 36 = 214 — продали билетов во второй кассе. Ответ: 178 и 214 билетов. 144. Пусть на Парковой улице было восстановлено х домов. Значит на Молодёжной улице восстановили х + 3 дома. На двух улицах восстановили х + х + 3 = 2х + 3 домов. 2х + 3 = 19 ⇒ 2х = 16 ⇒ х = 8 — восстановили на Парковой улице, х + 3 = 11 — восстановили на Молодёжной улице. Ответ: 8 восстановили на Парковой улице и 11 восстановили на Молодёжной улице. 145. Пусть одна из равных сторон треугольника х вторая равная ей тоже х, тогда третья сторона х - 2,9. Значит х + х + х - 2,9 = 16 ⇒ 3х = 18,9 ⇒ х = 6,3 ⇒ х - 2,9 = 3,4. Ответ: 6,3 см 6,3 см и 3,4 см. 146. Пусть протяжённость первого туннеля х, длинна второго тогда х + 17. Протяжённость двух туннелей равна: 6940 - 703 = 6237. Значит х + 17 + х = 6237 ⇒ 2х = 6220 ⇒ х = 3110 ⇒ х + 17 = 3127. Ответ: 3110 и 3127 метров. 147. Пусть первый жертвователь дал х рупий, тогда второй 2х, третий 3 • (2х) = 6х и четвёртый 4 х (3 • (2х)) = 4 • (6х) = 24х. Вместе они дали 132 рупий. Значит х + 2х + 6х + 24х = 132 ⇒ 3х + 30х = 132 ⇒ 33х = 132 ⇒ х = 4 ⇒ 2х = 8 ⇒ 6х = 24 ⇒ 24х = 96. Ответ: 4, 8, 24, и 96 рупий. 148. Пусть второй изготовил х деталей, тогда первый изготовил 1,15х деталей. Значит х + 1,15х = 86 ⇒ 2,15х = 86 ⇒ x = 149. Пусть прибыль, полученная в первом квартале х, тогда во втором 1,1х. Прибыль за два квартала составила 126000 р, значит 1,1х + х = 126000 ⇒ 2,1х = 126000 ⇒ х = 60000 ⇒ 1,1х = 66000 ⇒ 60 000 + 66 000 = 126 000. Ответ: в первом квартале 60000 р. 150. Пусть первая школа получила х компьютеров, тогда вторая x + б и третья х + 6 + 10. Три школы получили 70 компьютеров, значит х + х + 6 + х + 6 + 10 = 70 ⇒ 3x + 22 = 70 ⇒ 3х = 48 ⇒ х = 16 ⇒ х + б = 22 ⇒ х + б + 10 = 32. Ответ: первая школа получила 16, вторая 22 и третья 32 компьютеров. 151. Пусть не шапку ушло х граммов шерсти, тогда на свитер 5х и на шарф х - 5. На свитер, шапку и на шарф израсходовали 555 г шерсти, значит х + 5х + х - 5 = 555 ⇒ 7х = 560 ⇒ х = 80 ⇒ 5х = 400 ⇒ х - 5 = 75. Ответ: На шапку ушло 80 г, на свитер 400 г и на шарф 75 г. 152. Пусть на первой полке будет х книг, тогда на второй х + 8 и не третей х - 5. Всего нужно расположить 158 книг. Значит х + х + 8 + х - 5 = 158 ⇒ 3х = 155. 155 не делится на цело на 3 так как сумма цифр равна 11 и не кратна 3. (Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.) Значит нельзя расположит 158 книг на трёх полках как сказано в условии. Ответ: нельзя. 153. Пусть в первом ящике х банок, тогда втретьем х + 9 и во втором х + 9 - 4. Всего нужно разложить 59 банок в 3 ящика. Значит х + х + 9 + х + 9 - 4 = 59 ⇒ 3х = 45 ⇒ х = 15 ⇒ х + 9 = 24 ⇒ х + 9 - 4 = 20. Ответ: можно разложить. 154. Пусть изначально на первом участке было 5а; кустов малины, тогда на втором х. После того как с первого участка пересадили на второй 22 куста, на первом стало 5а - 22 кустов, а на втором х + 22 кустов и кустов на двух участках стало поровну. Значит 5x - 22 = х + 22 ⇒ 4х = 44 ⇒ х = 11 ⇒ 5х = 55. Ответ: на первом участке было 55 кустов, на втором 11 кустов. 155. Пусть скорость теплохода равна υT, а скорость течения реки vp. Скорость теплохода относительно берега против течения реки равна υT — υр. Скорость теплохода относительно берега по течению реки равна υT + υр. 156. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения и скорость течения реки υр = 2 км/ч. Значит 11 • (υT - 2) = 9 • (υT + 2) ⇒ 11υT - 22 = 9υT + 18 ⇒ 2υT = 40 ⇒ υT = 20. Ответ: υT = 20 км/ч. <<< К началу Решенния (окончание) >>>
|
|
|



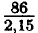 = 40 ⇒ 1,15х = 46. Ответ: первый деталей, второй изготовил 40 деталей.
= 40 ⇒ 1,15х = 46. Ответ: первый деталей, второй изготовил 40 деталей.