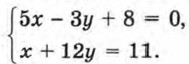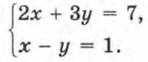|
|
|
|
|
Глава 3. Системы двух линейных уравнений с двумя переменными
§ 12. Метод подстановки (окончание)
Пример 1. Решить систему уравнений:
Р е ш е н и е. 1) Из первого уравнения системы получаем у = 3х - 5. 2) Подставим найденное выражение вместо у во второе уравнение системы: 2х + (3х - 5) - 7 = 0. 3) Решим полученное уравнение: 2х + 3х - 5 - 7 = 0; 5х - 12 = 0; 5х = 12;
4) Подставим найденное значение х в формулу у = 3х - 5:
5) Пара О т в е т: (2,4; 2,2). Вы узнали эту систему? Мы с ней встретились в предыдущем параграфе (система (5)), пробовали решить её графическим методом, и у нас ничего не получилось. Зато метод подстановки нас выручил. Он активно применяется и в более сложных системах уравнений, не обязательно линейных; о таких системах речь впереди — в старших классах. Этот метод, быть может, не всегда эффективен (т. е. не всегда быстро приводит к цели), но достаточно надёжен.
Пример 2. Решить систему уравнений:
Р е ш е н е. 1) Выразим х через у из второго уравнения: x = 11 - 12 у. 2) Подставим найденное выражение вместо х в первое уравнение системы: 5(11 - 12у) - 3у + 8 = 0. 3) Решим полученное уравнение: 55 - 60у - 3у + 8 = 0; 63 - 63у = 0; 63у = 63; y = 1. 4) Подставим найденное значение у в формулу х = 11 - 12у: х = 11 - 12 • 1 = -1. 5) Пара х = -1, у = 1 — единственное решение заданной системы. О т в е т: (-1; 1). Вопросы для самопроверки 1. Расскажите, в чём суть метода подстановки при решении системы двух линейных уравнений с двумя переменными. 2. Опишите алгоритм решения системы двух линейных уравнений с двумя переменными методом подстановки на примере решения системы
|
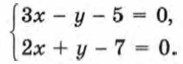
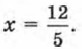
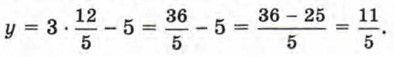
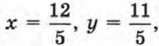т. е. х = 2,4, у = 2,2, — единственное решение заданной системы.
|
|