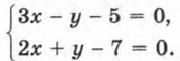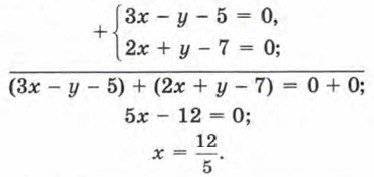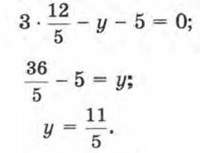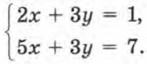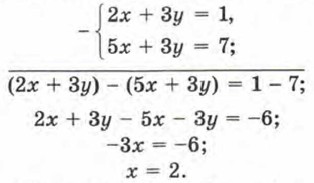§ 13. Метод алгебраического сложения

Мы довольно часто возвращаемся к тому, что уже обсудили ранее, например для того, чтобы рассмотреть ситуацию под другим углом зрения. Вот и теперь давайте вернёмся к примеру 1 из § 12, где речь шла о решении системы уравнений

Как мы решали эту систему? Мы выразили у из первого уравнения и подставили результат во второе, что привело к уравнению с одной переменной х, т. е. фактически к временному исключению из рассмотрения переменной у. Но исключить у из рассмотрения можно было значительно проще — достаточно сложить оба уравнения системы (сложить уравнения — это значит по отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять):

Затем можно было найденное значение х подставить в любое уравнение системы, например в первое, и найти у:

Попробуем применить аналогичные рассуждения ещё для нескольких систем линейных уравнений с двумя переменными.

Пример 1. Решить систему уравнений:

Р е ш е н и е. 1) Вычтем второе уравнение из первого:

2) Подставим найденное значение х = 2 в первое уравнение заданной системы, т. е. в уравнение 2х + 3у = 1:

2 • 2 + 3y = 1;

3у = 1 - 4;

3у = -3;

y = -1.

3) Пара х = 2, у = -1 — решение заданной системы.

О т в е т: (2; -1).

Окончание >>>