|
|
|
|
|
Глава 3. Системы двух линейных уравнений с двумя переменными § 13. Метод алгебраического сложения (окончание)Пример 2. Решить систему уравнений
Р е ш е н и е. Здесь сразу исключить переменную х или переменную у из обоих уравнений с помощью сложения или вычитания уравнений не удастся. Нужен подготовительный этап. Сначала умножим все члены первого уравнения системы на 3, а все члены второго уравнения — на 4. Получим
Теперь можно сложить уравнения, что приведёт к исключению переменной у. Имеем 17х = 43, т. е. Подставим найденное значение х во второе уравнение исходной системы, т. е. в уравнение 2х + 3y = 7:
Краткая запись приведённого решения:
Здесь справа от вертикальной черты записаны дополнительные множители, с помощью которых удалось уравнять абсолютные величины коэффициентов при переменной у в обоих уравнениях системы. Метод, который мы обсудили в этом параграфе, называют методом алгебраического сложения. Вопросы для самопроверки 1. Расскажите, в чём суть метода алгебраического сложения при решении системы двух линейных уравнений с двумя переменными. 2. Прокомментируйте метод алгебраического сложения на примере решения системы уравнении: 3. Решите систему уравнении 4. Как вы считаете, в каких случаях при решении системы линейных уравнений с двумя переменными удобнее использовать метод алгебраического сложения, чем метод подстановки?
|
|
|



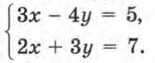
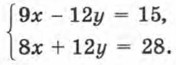
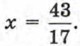
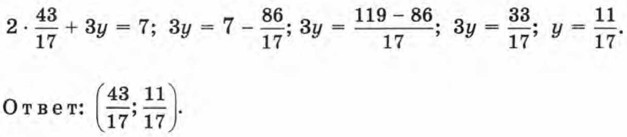
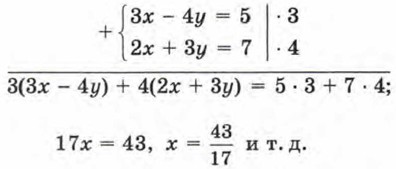

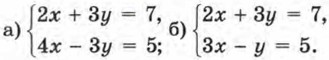
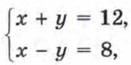 дважды применив метод алгебраического сложения.
дважды применив метод алгебраического сложения.