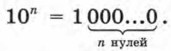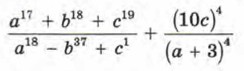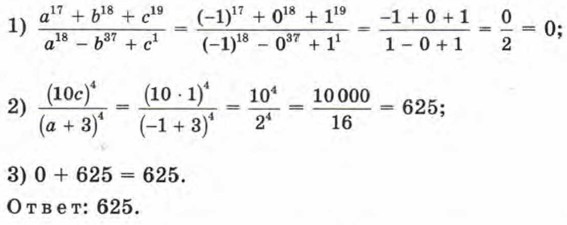Главная >> Алгебра 7 класс Мордкович

Глава 4. Степень с натуральным показателем и её свойства

§ 16. Таблица основных степеней

Вы знаете таблицу умножения, в неё включены произведения любых двух однозначных чисел (3 • 5, 4 • 7 и т. д.), этой таблицей вы постоянно пользуетесь при вычислениях. На практике полезна и таблица степеней простых однозначных чисел (в пределах тысячи). Составим её.

21 = 2 22 = 4 23 = 8 24 = 16 25 = 32 26 = 64 27 = 128 28 = 256 29 = 512 210 = 1024

31 = 3 32 = 9 33 = 27 34 = 81 35 = 243 36 = 729

51 = 5 52 = 25 53 = 125 54 = 625

71 = 7 72 = 49 73 = 343

С помощью этой таблицы можно находить и степени составных чисел (поэтому такие степени в таблицу обычно не включают). Например:

9³ = 9 • 9 • 9 = (3 • 3)(3 • 3)(3 • 3) = 3 • 3 • 3 • 3 • 3 • 3 = 3⁶ = 729.

Пример 1. Известно, что 2ⁿ = 128, 3^k = 243. Что больше: n или k?

Р е ш е н и е. По таблице находим, что 128 = 2⁷, значит, n = 7. По таблице также находим, что 243 = 3⁵, значит, k = 5. Так как 7 > 5, то n > k.

О т в е т: n > k.

1n = 1 для любого n; 0n = 0 для любого n; если n — чётное число (n = 2, 4, 6, 8, ...), то (-1)n = 1; если n — нечётное число (n = 1, 3, 5, 7, ...), то (-1)n = -1.

Кстати, используя формулу чётного числа n = 2k и формулу нечётного числа п = 2k - 1, можем записать, что

(-1)2k - 1; (-1)2k - 1 = -1.

А теперь выберем в качестве основания степени число 10:

10¹ = 10, 10² = 100, 10³ = 1000.

Обратите внимание: каков показатель, столько нулей надо записать после цифры 1.

Вообще

Например, 10⁶ = 1 000 000, 100 000 = 10⁵.

Пример 2. Найти значение выражения

при а = -1, b = 0, с = 1.

Р е ш е н и е.

В заключение данного параграфа ещё раз отметим, что математики всегда стремятся к краткости записей, чёткости рассуждений. Поэтому, введя новое понятие, они начинают изучать его свойства, а затем применяют эти свойства на практике.

О разных свойствах степени с натуральным показателем поговорим в следующем параграфе, а пока, забегая вперёд, заметим, что если бы одно из таких свойств мы уже знали, то не вычисляли бы так долго 9³, как это было сделано выше. Мы бы записали так:

9³ = (3²)³ = 3⁶ = 729.

Видите, запись в два раза короче. А почему это так, узнаете в § 17.

Вопросы для самопроверки

1. Чему равно значение выражения (-1)²⁰¹²? (-1)²⁰¹³?

2. Сколько нулей содержится в записи числа 10²⁰¹²?

3. Что больше: 0¹⁰⁰⁰ или 1¹⁰?