|
|
|
|
|
Глава 4. Степень с натуральным показателем и её свойства § 18. Умножение и деление степеней с одинаковыми показателями (окончание)
Пример 3. Упростить выражение Р е ш е н и е. Имеем
далее (22a3b4)5 = (22)5(a3)5(b4)5 (правило 4). Но (2 )5 = 210 = 1024; (a3)5 = a15; (b4)5 = b20 (правило 3). Значит, (22a3b4)5 = 1024a15b20. Так как 35 = 243, то окончательно получаем В заключение — одно предостережение. Мы знаем, что:
Если же умножение и деление выполняется над степенями с различными основаниями и разными показателями, то будьте внимательны. Так, 35 • 24 можно вычислить «в лоб»: сначала вычислить 35, затем 24 и, наконец, выполнить умножение. А можно так: 3 • 34 • 24 = 3 • (3 • 2)4 = 3 • 64. Вопросы для самопроверки 1. Закончите предложение: «Чтобы перемножить степени с одинаковыми показателями ...». 2. Закончите предложение: «Чтобы разделить друг на друга степени с одинаковыми показателями ...». 3. Запишите каждое из сформулированных вами в п. 1 и 2 правил на математическом языке. 4. Верно ли, что 35 • 45 = 125? Если да, то сошлитесь на соответствующее свойство степеней. 5. Верно ли, что 6. Верно ли, что 285 = 25 • 25 • 75? Если да, то сошлитесь на соответствующее свойство степеней. 7. Запишите число 330 в виде степени с основанием 27.
|
|
|



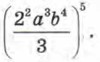
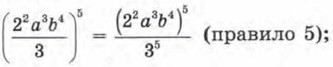
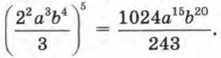


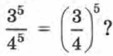 Если да, то сошлитесь на соответствующее свойство степеней.
Если да, то сошлитесь на соответствующее свойство степеней.