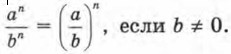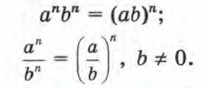|
|
|
|
|
Глава 4. Степень с натуральным показателем и её свойства § 18. Умножение и деление степеней с одинаковыми показателямиВ предыдущем параграфе мы рассматривали умножение и деление степеней с одинаковыми основаниями. Оказывается, можно умножать и делить степени и с разными основаниями, если только показатели у этих степеней одинаковые. Пример 1. Вычислить 24 • 54. Р е ш е н и е. Конечно, можно по таблице из § 16 установить, что 24 = 16 , 54 = 625, а затем умножить 16 на 625. Однако эффективнее следующее рассуждение: 24 • 54 = (2 • 2 • 2 • 2) • (5 • 5 • 5 • 5) = (2 • 5) • (2 • 5) • (2 • 5) • (2 • 5) = (2 • 5)4 = 104 = 10 000. В процессе решения мы получили числовое равенство 24 • 54 = (2 • 5)4. Точно так же можно доказать, что а3b3 = (аb)3. В самом деле, а3b3 = (а • а • а) • (b • b • b) = ab • ab • ab = (ab)3. Вообще имеет место равенство аnbn = (аb)n. Для тех, кому интересно, приведём «молчаливое» доказательство этого утверждения. Попробуйте его «озвучить» и прокомментировать:
Пример 2. Вычислить Р е ш е н и е. Конечно, можно производить вычисления «в лоб», т. е. найти 126, затем 46, затем первое число разделить на второе. Но лучше рассуждать так:
В процессе решения мы получили числовое равенство
Обе эти формулы применяют как слева направо, так и справа налево. Их также можно оформить в виде правил действий над степенями, тогда к трём правилам из § 17 добавятся ещё два:
|
|
|




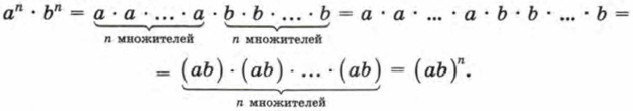
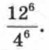
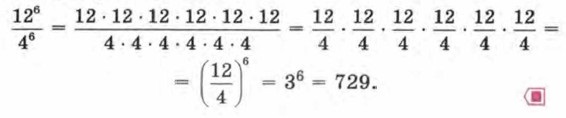
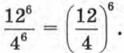 Точно так же можно доказать, что
Точно так же можно доказать, что 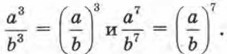 Вообще имеет место равенство
Вообще имеет место равенство