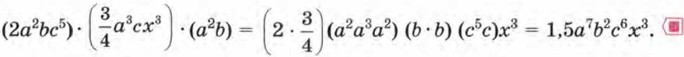|
|
|
|
|
Глава 5. Одночлены. Арифметические операции над одночленами § 22. Умножение одночленов. Возведение одночлена в натуральную степеньВ § 21 мы рассматривали сложение и вычитание одночленов. Оказалось, что эти операции применимы только к подобным одночленам. А как обстоит дело с умножением одночленов? Очень просто: если между двумя одночленами поставить знак умножения, то снова получится одночлен; остаётся лишь привести его к стандартному виду (фактически это мы уже делали в примере из § 20). Не вызывает затруднений и возведение одночлена в степень. При этом используются правила действий со степенями (фактически в примере 3 из § 18 мы уже возводили одночлен в степень, см. с. 94). Все правила действий над буквенными выражениями определяются таким образом, чтобы не менялись значения этих выражений при любой подстановке допустимых значений переменных. Пример 1. Найти произведение трёх одночленов: 2а2bс5, Р е ш е н и е.
Пример 2. Упростить выражение (-2а2bс3)5 (т. е. представить его в виде одночлена). Решение. (-2а2bс3)5 = -25(a2)5b5(c3)5 = -32a10b5c15. Мы использовали, во-первых, то, что при возведении произведения в степень надо возвести в эту степень каждый множитель. Поэтому у нас появилась запись 25(а2)5b5(с3)5. Во-вторых, мы воспользовались тем, что (-2)5 = -25. В-третьих, мы использовали то, что при возведении степени в степень показатели перемножаются. Поэтому вместо (а2)5 мы написали а10, а вместо (с3)5 мы написали с15. Пример 3. Представить одночлен 36а2b4с5 в виде произведения одночленов. Р е ш е н и е. Здесь, как и в примере 2 из § 21, решение не единственное. Вот несколько вариантов решения: 36a2b4c5 = (18a2) • (2b4c5);
Попробуйте сами придумать ещё несколько решений примера 3. Пример 4. Представить данный одночлен А в виде Вn, где В — одночлен, если: а) А = 32а5, n = 5;
|
|
|



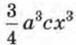 и а2b.
и а2b.