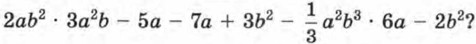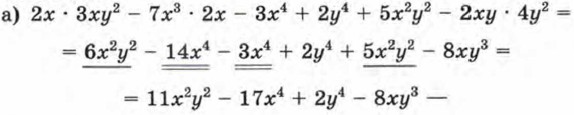Основные понятия многочлена (окончание)

Теперь вы понимаете, почему завись 4а³b³ - 12а + b² предпочтительнее первоначальной записи:

Дело в том, что первоначальная запись — не стандартный вид многочлена, а 4а³b³ - 12а + b² — стандартный вид.

Любой многочлен можно привести к стандартному виду. Условимся в дальнейшем всегда с этого начинать — так удобнее производить действия с многочленами.

Обычно многочлен обозначают буквой р или Р — с этой буквы начинается греческое слово polys («многий», «многочисленный»; многочлены в математике называют также полиномами). В обозначение включают и переменные, из которых состоят члены многочлена. Например, многочлен 2х² - 5х + 3 обозначают р(х) — читают: «пэ от икс»; многочлен 2х² + 3ху - у⁴ обозначают р(х; у) — читают: «пэ от икс, игрек» и т. д.

Пример. Дан многочлен

р(х; у) = 2х • 3ху² - 7х³ • 2х - 3х⁴ + 2у⁴ + bх²у² - 2ху • 4у².

а) Записать его в стандартном виде;

б) вычислить: р(1; 2); р(-1; 1); р(0; 1).

Р е ш е н и е.

это стандартный вид многочлена.

б) Запись р(1; 2) означает, что нужно найти значение многочлена р(х; у) при х = 1, у = 2. Вычисления будем производить для многочлена, записанного в стандартном виде:

р(х; у) = 11 х²у² - 17х⁴ + 2у⁴ - 8ху³.

Имеем

р(1; 2) = 11 • 1² • 2² - 17 • 1⁴ + 2 • 2⁴ - 8 • 1 • 2³ = 44 - 17 + 32 - 64 = -5.

Итак, р(1; 2) = -5.

Аналогично

р(-1; 1) = 11 • (-1)² • 1² - 17 • (-1)⁴ + 2 • 1⁴ - 8 • (-1) • 1³ = 11 - 17 + 2 + 8 = 4,

т. е. р(-1; 1) = 4.

Наконец,

р(0; 1) = 11 • 0² • 1² - 17 • 0⁴ + 2 • 1⁴ - 8 • 0 • 1³ = 0 - 0 + 2 - 0 = 2.

Итак, р(0; 1) = 2.

Вопросы для самопроверки

1. Что такое многочлен?

2. Опишите процесс приведения многочлена к стандартному виду. Прокомментируйте это на примере приведения к стандартному виду многочлена 2аbаbс - 3abcb² + 4bcbab + 5а²bсb.

3. Если р(х; у) = 3х²у - 2ху² + 2х - 3у, то чему равно р(1; -1)?

4. Приведите пример многочлена, у которого есть взаимно уничтожающиеся члены.

<<< К началу