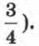§ 25. Сложение и вычитание многочленов

В предыдущем параграфе мы ввели понятия многочлена и стандартного вида многочлена. Вы уже, наверное, начинаете привыкать к тому, что, введя новое понятие, надо учиться работать с ним. В частности, будем учиться выполнять арифметические операции над многочленами.

Начинаем со сложения и вычитания. Это очень простые операции: чтобы сложить несколько многочленов, их записывают в скобках со знаком «+» между скобками, раскрывают скобки и приводят подобные члены. При вычитании одного многочлена из другого их записывают в скобках со знаком «-» перед вычитаемым, раскрывают скобки и приводят подобные члены.

Пример 1. Сложить многочлены:

а) p₁(x) = 2х² + 3х - 8, р₂(х) = 5х + 2;

б) р₁(а; b) = а² + 2ab - b², р₂(а; b) = 2а³ - а² + 3ab - b² + 5, р₃(а; b) = а² - ab - b² - 4.

Р е ш е н и е.

а) Обозначим сумму многочленов через р(х). Тогда

р(х) = р₁(х) + р₂(х) = (2х² + 3х - 8) + (5x + 2) = 2х² + 3х - 8 + 5x + 2 = 2х² + (3х + 5х) + (-8 + 2) = 2х² + 8х - 6.

б) Обозначим сумму многочленов через р(а; b). Тогда

Пример 2. Найти разность многочленов

р₁(x; у) = х³ + у³ + 2х + 3у + 5

р₂(х; у) = х³ - у³ - 5х + 3у - 7.

Р е ш е н и е. Обозначим разность многочленов через р(х; у). Тогда

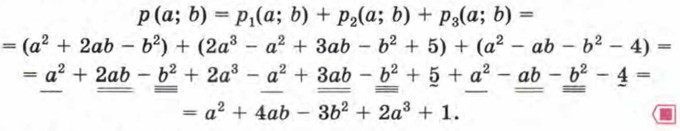
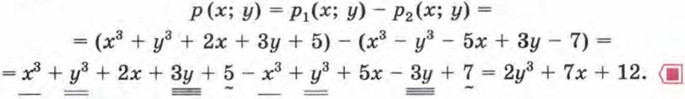
Обратите внимание: х³ - х³ = 0 и 3у - 3у = 0. Поэтому «исчезли» одночлен х³ и одночлен Зу из состава обоих многочленов. В таких случаях говорят: х³ и -х³, 3у и -3у взаимно уничтожились (правда, школьники в таких случаях любят говорить «сократились», но так говорить не следует: термин «сокращение» в математике принято употреблять только по отношению к дробям; например, можно сократить дробь 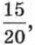и тогда получится

Окончание >>>