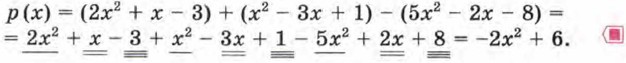§ 25. Сложение и вычитание многочленов (окончание)

Заметим, что сложение и вычитание многочленов выполняются по одному и тому же правилу, т. е. необходимости в различении операций сложения и вычитания нет, значит, нет и особой необходимости в использовании двух терминов: «сложение многочленов», «вычитание многочленов». Вместо них можно употребить термин алгебраическая сумма многочленов. Вот несколько примеров алгебраических сумм трёх многочленов р₁(х), р₂(х), р₃(х):

p₁(x) + р₂(х) + р₃(х);

p₁(x) - р₂(х) + р₃(х);

p₁(x) - р₂(х) - р₃(х);

р₂(х) - р₃(х) + р₁(х).

Теперь мы можем подвести итог всему сказанному в этом параграфе в виде следующего правила составления алгебраической суммы многочленов.

Правило 1. Чтобы записать алгебраическую сумму нескольких многочленов в виде многочлена стандартного вида, нужно раскрыть скобки и привести подобные члены. При этом если перед скобкой стоит знак «+», то при раскрытии скобок надо знаки, стоящие перед слагаемыми в скобках, оставить без изменения. Если же перед скобкой стоит знак «-», то при раскрытии скобок нужно знаки, стоящие перед слагаемыми в скобках, заменить на противоположные («+» на «-», «-» на «+»).

А теперь обязательно вернитесь к примерам 1 и 2 и прокомментируйте (хотя бы для себя) их решение с помощью этого правила. Сделали? Тогда рассмотрим заключительный пример.

Пример 3. Даны три многочлена:

p₁(x) = 2х² + х - 3; р₂(х) = х² - 3х + 1; р₃(x) = 5х² - 2х - 8.

Найти алгебраическую сумму

р(х) = р₁(х) + р₂(х) - р₃(х).

Р е ш е н и е.

Вопросы для самопроверки

1. Может ли сумма двух многочленов быть одночленом? Если да, то приведите пример.

2. Может ли разность двух многочленов быть одночленом? Если да, то приведите пример.

3. Всегда ли задание найти сумму или разность многочленов является корректным?

4. Может ли сумма или разность двух многочленов равняться числу? Если да, то приведите пример.

<<< К началу