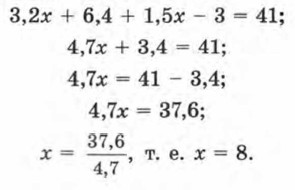|
|
|
|
|
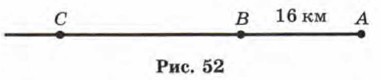
Глава 6. Многочлены. Арифметические операции над многочленами § 26. Умножение многочлена на одночлен (окончание)Пример 3. Пункты А, В и С расположены на шоссе так, как показано на рисунке 52. Расстояние между А и В равно 16 км. Из В по направлению к С вышел пешеход. Через 2 ч после этого из А по направлению к С выехал велосипедист, скорость которого на 6 км/ч больше скорости пешехода. Через 4 ч после своего выезда велосипедист догнал пешехода в пункте С. Чему равно расстояние от В до С?
Р е ш е н и е. Первый этап. Составление математической модели. Пусть х км/ч — скорость пешехода, тогда (х + 6) км/ч — скорость велосипедиста. Расстояние от А до С велосипедист проехал за 4 ч, значит, это расстояние выражается формулой 4(х + 6) км. Итак, АС = 4(х + 6). Расстояние oт В до С пешеход прошёл за 6 ч (ведь до выезда велосипедиста он уже был в пути 2 ч), следовательно, это расстояние выражается формулой 6х км. Итак, ВС = 6х. А теперь обратите внимание на рисунок 52: АС - ВС = АВ, т. е. АС - ВС = 16. Это — основа для составления математической модели задачи. Напомним, что АС = 4(х + 6), ВС = 6х; следовательно, 4(х + 6) - 6х = 16. Второй этап. Работа с составленной моделью. Для решения уравнения придётся, во-первых, умножить одночлен 4 на двучлен х + 6, получим 4х + 24. Во-вторых, придётся из двучлена 4х + 24 вычесть одночлен 6х: 4х + 24 - 6х = 24 - 2х. После этих преобразований уравнение примет более простой вид: 24 - 2х = 16. Далее имеем -2х = 16 - 24;
Третий этап. Ответ на вопрос задачи. Мы получили, что x = 4, значит, скорость пешехода 4 км/ч. Но нам нужно найти не это, в задаче требуется найти расстояние от В до С. Мы установили, что ВС = 6x; значит, ВС = 6 • 4 = 24. О т в е т: расстояние от В до С равно 24 км. Пример 4. Лодка плыла по течению реки 3 ч 12 мин, а затем против течения 1,5 ч. Найти собственную скорость лодки (т. е. скорость в стоячей воде), если известно, что скорость течения реки 2 км/ч, а всего лодкой пройден путь 41 км. Р е ш е н и е. Первый этап. Составление математической модели. Пусть х км/ч — собственная скорость лодки, тогда по течению она плывёт со скоростью (х + 2) км/ч (течение помогает), а против течения — со скоростью (x - 2) км/ч (течение препятствует). По течению реки лодка плыла 3 ч 12 мин. Поскольку скорость выражена в километрах в час, это время надо записать в часах. Имеем Против течения лодка плыла 1,5 ч. За это время со скоростью (х - 2) км/ч лодкой пройден путь 1,5(x - 2) км. По условию весь её путь равен 41 км. Так как он состоит из пути по течению и пути против течения, то получаем 3,2(x + 2) + 1,б(х - 2) = 41. Это уравнение — математическая модель задачи. Второй этап. Работа с математической моделью. Как всегда, на этом этапе думаем только о том, как решить модель — уравнение, а не о том, откуда эта модель взялась. Выполним в левой части уравнения умножение одночлена 3,2 на двучлен х + 2, одночлена 1,5 на двучлен х - 2, а затем полученные многочлены (двучлены) сложим:
Третий этап. Ответ на вопрос задачи. Спрашивается, чему равна собственная скорость лодки, т. е. чему равен х. Но ответ на этот вопрос уже получен: х = 8. О т в е т: собственная скорость лодки 8 км/ч. Вопросы для самопроверки 1. Сформулируйте правило умножения многочлена на одночлен. Проиллюстрируйте его на придуманном вами примере умножения трёхчлена на одночлен. 2. Всегда ли задание представить заданный многочлен в виде произведения многочлена и одночлена является корректным?
|
|
|



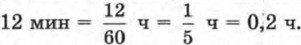 Значит, 3 ч 12 мин= 3,2 ч. За это время со скоростью (x + 2) км/ч лодкой пройден путь 3,2(x + 2) км.
Значит, 3 ч 12 мин= 3,2 ч. За это время со скоростью (x + 2) км/ч лодкой пройден путь 3,2(x + 2) км.