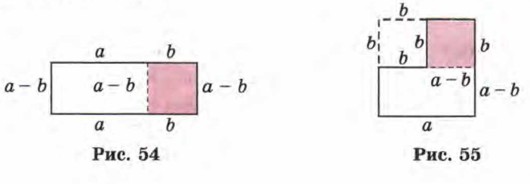§ 28. Формулы сокращённого умножения (продолжение)

2. Разность квадратов

Умножим двучлен а + b на двучлен а - b:

(а + b) (а - b) = а² - аb + bа - b² - а² - b².

Итак,

(а + b) (а - b) = а² - b². (3)

Любое равенство в математике употребляют как слева направо (т. е. левая часть равенства заменяется его правой частью), так и справа налево (т. е. правая часть равенства заменяется его левой частью). Если формулу (3) использовать слева направо, то она позволяет заменить произведение (а + b)(а - b) готовым результатом а² - b². Эту же формулу можно использовать справа налево, тогда она позволяет заменить разность квадратов а² - b² произведением (а + b) (а - b). Формуле (3) в математике дано специальное название — разность квадратов.

Замечание. Не путайте термины «разность квадратов» и «квадрат разности». Разность квадратов — это а² - b², значит, речь идёт о формуле (3); квадрат разности — это (а - b)², значит, речь идёт о формуле (2).

На обычном языке формулу (3) читают справа налево так:

разность квадратов двух выражений равна произведению суммы этих выражений на их разность.

Пример 2. Выполнить умножение:

(3х - 2у) (3х + 2у).

Р е ш е н и е.

(3х - 2у) (3х + 2у) = (3х)² - (2у)² = 9х² - 4y².

Пример 3. Представить двучлен 16х⁴ - 9 в виде произведения двучленов.

Р е ш е н и е.

Имеем 16х⁴ = (4х²)², 9 = 3², значит, заданный двучлен есть разность квадратов, т. е. к нему можно применить формулу (3), прочитанную справа налево. Тогда получим

16х⁴ - 9 = (4х²)² - 3² = (4х² + 3) (4х² - 3).

Формула (3), как и формулы (1) и (2), используется иногда для быстрого счёта. Смотрите:

79 • 81 = (80 - 1) (80 + 1) = 802 - 1² = 6400 - 1 = 6399;

42 • 38 = (40 + 2) (40 - 2) = 402 - 2² = 1600 - 4 = 1596.

Завершим разговор о формуле разности квадратов любопытным геометрическим рассуждением. Пусть а и b — положительные числа, причём а > b. Рассмотрим прямоугольник со сторонами а + b и а - b (рис. 54). Его площадь равна (а + b) (а - b). Отрежем прямоугольник со сторонами b и а - b и подклеим его к оставшейся части так, как показано на рисунке 55. Ясно, что полученная фигура имеет ту же площадь, т. е. (а + b) (а - b). Но эту фигуру можно построить так: из квадрата со стороной а вырезать квадрат со стороной b (это хорошо видно на рис. 55). Значит, площадь новой фигуры равна а² - b². Итак, (а + b) (а - b) = а² - b², т. е. получили формулу (3).

<<< К началу Окончание >>>