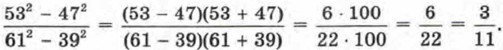|
|
|
|
|
Глава 7. Разложение многочленов на множители § 30. Что такое разложение многочленов на множители и зачем оно нужноДля начала выполним знакомую операцию: умножим многочлен 2х - 3 на многочлен х + 2. (2х - 3) (х + 2) = 2х • х + 2х • 2 - 3 • х - 3 • 2 = 2х2 + 4х - 3х - 6 = 2х2 + x - 6. Итак, (2х - 3) (х + 2) = 2х2 + х - 6. Это равенство можно записать по-другому, поменяв его части местами: 2х2 + х - 6 - (2x - 3) (x + 2).
Такая запись означает, что многочлен 2х2 + х - 6 представлен в виде произведения более простых многочленов 2х - 3 и х + 2. Обычно в таких случаях говорят, что многочлен удалось разложить на множители. На самом деле формулировка «разложение многочлена на множители» вам уже знакома, мы несколько раз использовали её в главе 6, но там же мы говорили, что позднее более подробно обсудим эту проблему (проблему разложения многочлена на множители). Это время пришло. Однако сначала убедимся в том, что разложение многочлена на множители — вещь полезная (иначе зачем нам этим заниматься?). Представьте себе, что вам предложили решить уравнение 2х - 3 = 0. Вы справитесь с этим без труда: 2х = 3, х = 1,5. Затем вам предложили решить уравнение х + 2 = 0. И с ним вы справитесь легко: х = -2. А теперь вам предлагают решить уравнение 2х2 + х - 6 = 0, т. е. дать ответ на вопрос, при каких значениях х трёхчлен 2х2 + х - 6 обращается в нуль, — эти значения х называют корнями уравнения. Для таких уравнений имеется специальное правило решения, но вы его пока не знаете. Как быть? Воспользуемся полученным выше разложением многочлена 2х2 + х - 6 на множители: 2х2 + х - 6 = (2х - 3)(x + 2). Тогда заданное уравнение можно переписать в виде (2х - 3)(х + 2) = 0. Теперь остаётся воспользоваться следующим известным фактом: если произведение двух множителей равно нулю, то один из множителей равен нулю. Значит, либо 2х - 3 = 0, либо х + 2 = 0. Задача свелась к решению двух более простых уравнений. Из уравнения 2х - 3 = 0 получаем х = 1,5. Из уравнения х + 2 = 0 получаем х = -2. Уравнение решено, оно имеет два корня: 1,5 и -2. Итак, разложение многочлена на множители может пригодиться нам для решения уравнений. Рассмотрим другую ситуацию. Пусть нужно найти значение числового выражения
Разложение на множители позволило нам сократить дробь. Позднее мы оценим это и при выполнении действий с алгебраическими дробями.
|
|
|




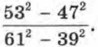 Можно, конечно, проводить вычисления «в лоб», но более эффективно дважды воспользоваться формулой разности квадратов:
Можно, конечно, проводить вычисления «в лоб», но более эффективно дважды воспользоваться формулой разности квадратов: