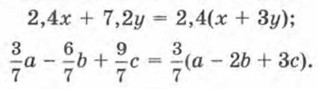§ 31. Вынесение общего множителя за скобки

Прежде чем начинать изучение этого параграфа, вернитесь к § 26. Там мы уже рассмотрели пример, в котором требовалось представить многочлен в виде произведения многочлена и одночлена. Если такое произведение удалось составить, то обычно говорят, что многочлен разложен на множители с помощью вынесения общего множителя за скобки. Рассмотрим несколько примеров.

Пример 1. Разложить на множители многочлен:

а) 2х + 6у;
б) а³ + а²;
в) 4а³ + 6а²;

г) 12аb⁴ - 18а²b³с;
д) 5а⁴ - 10а³ + 15а⁵.

Р е ш е н и е.

а) 2х + 6у = 2(х + 3у). За скобки вынесли общий делитель коэффициентов членов многочлена.

б) а³ + а² = а² (а + 1). Если одна и та же переменная входит во все члены многочлена, то её можно вынести за скобки в степени, равной наименьшей из имеющихся (т. е. выбирают наименьший из имеющихся показателей).

в) Здесь используем те же приёмы, что и при решении примеров а) и б): для коэффициентов находим общий делитель (в данном случае число 2), для переменных — наименьшую степень из имеющихся (в данном случае а²). Получаем

4а³ + 6а² = 2а² • 2а + 2а² • 3 = 2а²(2а + 3).

г) Обычно для целочисленных коэффициентов стараются найти не просто общий делитель, а наибольший общий делитель. Для коэффициентов 12 и 18 им будет число 6. Замечаем, что переменная а входит в оба члена многочлена, при этом наименьший показатель равен 1. Переменная b также входит в оба члена многочлена, причём наименьший показатель равен 3. Наконец, переменная с входит только во второй член многочлена и не входит в первый член, значит, эту переменную нельзя вынести за скобки ни в какой степени. В итоге получаем

12аb⁴ - 18а2b³с = 6аb³ • 2b - 6аb³ • 3ас = 6аb³(2b - 3ас).

д) 5а⁴ - 10а³ + 15а⁵ = 5а³(а - 2 + 3а²).

В этом примере мы фактически использовали следующий алгоритм.

Алгоритм отыскания общего множителя нескольких одночленов
1. Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, — он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
2. Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
3. Произведение коэффициента, найденного на первом шаге, и степеней, найденных на втором шаге, является общим множителем, который целесообразно вынести за скобки.

Замечание 1. В ряде случаев полезно выносить за скобку в качестве общего множителя и дробный коэффициент. Например:

Замечание 2. Следует понимать, что шаги 1 и 2 алгоритма имеют совершенно разный статус. В реальных задачах коэффициенты почти никогда не бывают целыми числами (а оказываются целыми благодаря усилиям составителей задачников, подбирающих условия так, чтобы ответ был покрасивее). Поэтому шаг 1 посвящён лишь получению наиболее приятной для глаза записи, тогда как шаг 2 есть нечто содержательное.

Окончание >>>