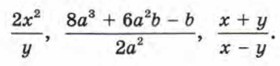|
|
|
|
|
Глава 7. Разложение многочленов на множители § 35. Сокращение алгебраических дробейНовое понятие в математике редко возникает «из ничего», «на пустом месте». Оно появляется тогда, когда в нём ощущается объективная необходимость. Именно так появились в математике отрицательные числа, так появились обыкновенные и десятичные дроби.
Предпосылки для введения нового понятия «алгебраическая дробь» у нас имеются. Давайте вернёмся к § 23. Обсуждая там деление одночлена на одночлен, мы рассмотрели ряд примеров. Выделим два из них. 1. Разделить одночлен 36а3b5 на одночлен 4ab2 (см. пример 1в) из § 23). Решали мы его так. Вместо записи 36а3b5 : 4ab2 использовали черту дроби:
2. Разделить одночлен 4х3 на одночлен 2ху (см. пример 1д) из § 23). Действуя по тому же образцу, мы получили
В § 23 мы отметили, что одночлен 4х3 не удалось разделить на одночлен 2ху так, чтобы получился одночлен. Но ведь математические модели могут содержать операцию деления любых одночленов, не обязательно таких, что один делится на другой. Поэтому математики ввели новое понятие — понятие алгебраической дроби. В частности,
Теперь вернёмся к § 29. Обсуждая там операцию деления многочлена на одночлен, мы отметили, что она не всегда выполнима. Так, в примере 2 из § 29 речь шла о делении двучлена 6x3 - 24х2 на одночлен 6х2. Эта операция оказалась выполнимой, и в результате мы получили двучлен х - 4. Значит,
Иными словами, алгебраическое выражение В то же время в примере 3 из § 29 не удалось разделить многочлен 8а3 + 6а2b — b на 2а2, т. е. выражение Что же касается операции деления многочлена на многочлен, то единственное, что мы можем сейчас сказать: один многочлен можно разделить на другой, если этот другой многочлен является одним из множителей в разложении первого многочлена на множители. Например, х3 - 1 = (х - 1) (х2 + х + 1). Значит, х3 - 1 можно разделить на х2 + х + 1, получится х - 1; х3 - 1 можно разделить на х - 1, получится х2 + х + 1.
Алгебраической дробью называют отношение двух многочленов Р и Q. При этом используют запись Примеры алгебраических дробей:
Иногда алгебраическую дробь удаётся заменить многочленом.
|
|
|




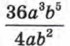 (ведь А: В и
(ведь А: В и 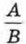 — одно и то же). Это позволило вместо записей 36 : 4, а3 : a, b5 : b2 также использовать черту дроби, что сделало решение примера более наглядным:
— одно и то же). Это позволило вместо записей 36 : 4, а3 : a, b5 : b2 также использовать черту дроби, что сделало решение примера более наглядным:
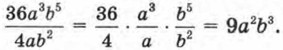
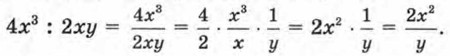
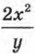 — алгебраическая дробь.
— алгебраическая дробь.
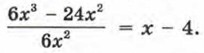
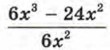 удалось заменить более простым выражением — многочленом х - 4.
удалось заменить более простым выражением — многочленом х - 4.
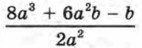 не удалось заменить более простым выражением, пришлось так и оставить его в виде алгебраической дроби.
не удалось заменить более простым выражением, пришлось так и оставить его в виде алгебраической дроби.

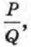 где Р — числитель, Q — знаменатель алгебраической дроби.
где Р — числитель, Q — знаменатель алгебраической дроби.