§ 38. Графическое решение уравнений

Подытожим наши знания о графиках функций. Мы с вами научились строить графики следующих функций:

у = b (прямую, параллельную оси х);

у = kx (прямую, проходящую через начало координат);

у = kx + m (прямую);

у = х², у = -х² (параболу).

Знание этих графиков позволит нам в случае необходимости заменить аналитическую модель геометрической (графической), например вместо модели у = х² (которая представляет собой равенство с двумя переменными х и у) рассматривать параболу в координатной плоскости. В частности, это иногда полезно для решения уравнений. Как это делается, обсудим на нескольких примерах.

Пример 1. Решить уравнение х² = х + 2.

Р е ш е н и е.

Рассмотрим функции у = х² и у = х + 2; построим их графики и найдём точки пересечения графиков. Эту задачу мы с вами уже решали (см. пример 2 из § 37 и соответственно рис. 61). Парабола у = х² и прямая у = х + 2 пересекаются в точках А(-1; 1) и В(2; 4).

Как же найти корни уравнения х² = х + 2, т. е. те значения х, при которых выражения х² и х + 2 принимают одинаковые числовые значения? Очень просто, эти значения уже найдены; х₁ = -1, х₂ = 2. Это абсциссы точек А и В, в которых пересекаются построенные графики.

О т в е т: x₁ = -1, х₂ = 2.

Фактически мы использовали следующий алгоритм.

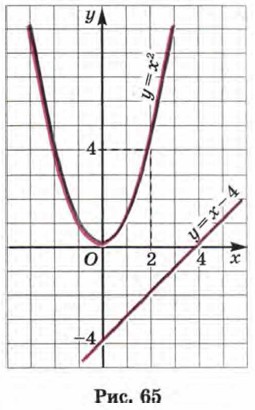
1. Ввели в рассмотрение функции у = х₂,у = х + 2 (для другого уравнения будут, разумеется, иные функции).

2. Построили в одной системе координат графики функций у = х₂, у = х + 2.

3. Нашли точки пересечения графиков.

4. Нашли абсциссы точек пересечения — это и есть корни уравнения.

Пример 2. Решить уравнение х₂ - х + 4 = 0.

Р е ш е н и е.

Здесь придётся дополнить выработанный алгоритм ещё одним шагом (подготовительным шагом): надо переписать уравнение в виде, для которого имеется алгоритм. Этот вид таков: х₂ = х - 4. Теперь всё в порядке, действуем в соответствии с алгоритмом.

1) Введём две функции: у = х₂, У = х- 4.

2) Построим в одной системе координат графики функций у = х₂ и у = = х - 4 (рис. 65).

3) Точек пересечения у построенных параболы и прямой нет.

Как вы думаете, что означает этот геометрический факт для данной алгебраической задачи (для данного уравнения)? Догадались? А теперь сопоставьте свою догадку с тем, что ниже записано в ответе.

О т в е т: уравнение не имеет корней.

Замечание. В § 34 мы уже говорили о том, что существуют так называемые квадратные уравнения — уравнения вида ах₂ + bх + с = О, где а, b, с — числа, а ≠ 0. Они решаются по специальным формулам для отыскания корней, но этих формул вы пока не знаете. Тем не менее некоторые квадратные уравнения мы уже решили. Так, в § 34 мы решили уравнение х₂ - 6х + 5 = 0 методом разложения на множители. А в настоящем параграфе мы решили ещё два квадратных уравнения — графическим методом. Это уравнение х₂ -х - 2 = 0 (см. пример 1; правда, там уравнение было записано по-другому: х₂ = х + 2 — но вы же понимаете, что это то же самое) и уравнение х₂ - х + 4 = 0 (см. пример 2).

Вопросы для самопроверки

1. Перечислите все функции, которые вы изучили в курсе алгебры 7-го класса.

2. Сформулируйте алгоритм решения уравнения вида ƒ(x) = g(x).

3. Что нужно сделать, чтобы графически решить уравнение вида х₂ = kx + m? Прокомментируйте свой ответ на примере решения уравнения х₂ = 2х + 3.

4. Установите, используя графический метод, сколько корней имеет уравнение: а) х₂ + х - 4 = 0; б) х₂ + х + 4 = 0.