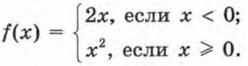§ 39. Что означает в математике запись у = ƒ(x)

Изучая какой-либо реальный процесс, обычно обращают внимание на две величины, участвующие в процессе (в более сложных процессах участвуют не две величины, а три, четыре и т.д., но мы пока такие процессы не рассматриваем): одна из них меняется как бы сама собой, независимо ни от чего (такую переменную чаще всего обозначают буквой х), а другая величина принимает значения, которые зависят от выбранных значений переменной х (такую зависимую переменную чаще всего обозначают буквой у). Математической моделью реального процесса как раз и является запись на математическом языке зависимости у от х, т. е. связи между переменными х и у.

Ещё раз напомним, что к настоящему моменту мы изучили следующие математические модели: у = b, у = kx, у = kx + m, у = х², у = -х². Есть ли у этих математических моделей что-либо общее? Есть! Их структура одинакова:

y = ƒ(x).

Эту запись («игрек равен эф от икс») следует понимать так: имеется выражение ƒ(x) с переменной х, с помощью которого мы находим значения переменной у.

Математики предпочитают запись у = ƒ(x) не случайно. Пусть, например, ƒ(x) = х², т. е. речь идёт о функции у = х². Пусть нам надо выделить несколько значений аргумента и соответствующих значений функции. До сих пор мы писали так:

если х = 1, то у = 1² = 1;

если х = -3, то у = (-3)² = 9 и т. д.

Если же использовать обозначение ƒ(x) = х², то запись становится более экономной:

ƒ(1) = 1² = 1;

ƒ(-3) = (-3)² = 9.

Итак, мы познакомились ещё с одним фрагментом математического языка: фраза «значение функции у = х² в точке х = 2 равно 4» записывается короче: «если ƒ(x) = х², то ƒ(2) = 4».

А вот образец обратного перевода.

Если ƒ(х) = х², то ƒ(-3) = 9. По-другому — значение функции у = х² в точке х = -3 равно 9.

Пример 1. Дана функция у = ƒ(х), где ƒ(х) = х³. Вычислить:

а) ƒ(1);
б) ƒ(-4);
в) ƒ(а);
г) ƒ(2а);
д) ƒ(а - 1);
е) ƒ(3x);
ж) ƒ(-х).

Р е ш е н и е.

Во всех случаях план действий один и тот же: нужно в выражении ƒ(х) подставить вместо х то значение аргумента, которое указано в скобках, и выполнить соответствующие вычисления и преобразования.

а) ƒ(1) = 1³ = 1; б) ƒ(-4) = (-4)³ = -64; в) ƒ(а) = а³; г) ƒ(2а) = (2а)³ = 8а³; д) ƒ(а - 1) = (а - 1)³; е) ƒ(3х) = (3х)³ = 27х³; ж) ƒ(-х) = (-х)³ = -х³.

Замечание. Разумеется, вместо буквы ƒ можно использовать любую другую букву (в основном из латинского алфавита): g(x), h(x), s(x) и т. д.

Пример 2. Даны две функции: у = ƒ(х), где ƒ(х) = х², и у = g(x), где g(х) = х³. Доказать, что:

а) ƒ(-х) = ƒ(х); б) g(-x) = -g(х).

Р е ш е н и е.

а) Так как ƒ(х) = х², то ƒ(-х) = (-х)² = х². Итак, ƒ(х) = х², ƒ(-х) = х², значит, ƒ(-х) = ƒ(х).

б) Так как g(x) = х³, то g(-x) = (-х)³ = -x³. Итак, g(x) = х³, g(-x) = -х³, т. е. g(-x) = -g(x).

Использование математической модели вида у = ƒ(x) оказывается удобным во многих случаях, в частности тогда, когда реальный процесс описывается различными формулами на разных промежутках изменения независимой переменной.

Пример 3. Дана функция у = ƒ(x), где

а) Вычислить: ƒ(-5), ƒ(-2), ƒ(1,5), ƒ(4), ƒ(0).

б) Построить график функции у = ƒ(x).

Р е ш е н и е.

а) Что такое ƒ(-5)? Это значение заданной функции в точке х = -5. Но функция задана не одним выражением, а двумя: 2х и х². Каким из них воспользоваться? Это зависит от выбранного значения аргумента. Мы выбрали х = -5, а число -5 удовлетворяет неравенству х < 0; в этом случае функция задаётся выражением, стоящим в первой строке, т. е. ƒ(x) = 2х. Тогда ƒ(-5) = 2 • (-5) = -10.

Аналогично вычисляем ƒ(-2): если х = -2, то х < 0 и, значит, ƒ(x) = 2х, т. е. ƒ(-2) = 2 • (-2) = -4.

Продолжение >>>