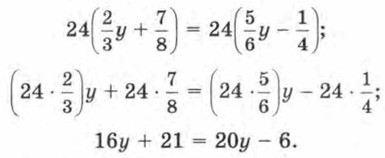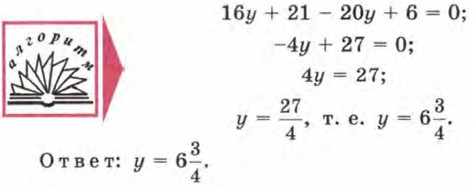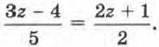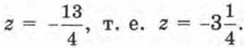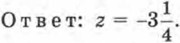§ 4. Линейное уравнение с одной переменной (окончание)

Второй способ. Прежде чем применять алгоритм, умножим обе части уравнения на 24 — это наименьший общий знаменатель имеющихся дробей. При этом мы пользуемся тем, что если А = В, то 24А = 24В, и обратно. Получим

А далее воспользуемся алгоритмом:

Пример 2. Решить уравнение

Р е ш е н и е. Воспользовавшись основным свойством пропорции (произведение крайних членов пропорции равно произведению средних членов), получим

2(3z - 4) = 5(2z + 1).

Дальнейший ход решения, надеемся, уже не требует комментариев:

6z - 8 - 10z -5 = 0;
-4z - 13 = 0;
-4z = 13;

Пример 3. Купили некоторое количество книг для библиотеки и пытаются разместить их на одинаковых полках стеллажа. Сначала поставили по 20 книг на каждую полку. В результате две полки оказались пустыми, а остальные заполненными (по 20 книг). Затем решили ставить по 15 книг на полку. Попытка оказалась удачной: все полки заполнились (по 15 книг на каждой). Сколько книг было куплено?

Первый этап. Составление математической модели.

Обозначим буквой х число полок в стеллаже. Когда на каждую полку поставили по 20 книг, то заполненными оказались (x - 2) полки. Значит, общее число купленных книг выражается формулой 20(x - 2). Далее в задаче сказано, что когда на каждую полку поставили по 15 книг, то все х полок оказались заполненными сплошь. Значит, общее число купленных книг выражается формулой 15x. Остаётся приравнять два полученных выражения числа купленных книг:

20(x - 2) = 15x.

Это уравнение — математическая модель задачи.

Второй этап. Работа с составленной математической моделью.

Решаем уравнение:

20(x - 2) - 15x = 0;
20x - 40 - 15x = 0;
5x - 40 = 0;
5x = 40;
x = 8.

Третий этап. Ответ на вопрос задачи.

Мы выяснили, что в стеллаже 8 полок. Все купленные книги разместились на этих полках по 15 штук на каждой. Значит, всего было куплено 15 • 8 = 120 книг.

О т в е т: всего было куплено 120 книг.

Вопросы для самопроверки

1. Что такое линейное уравнение с одной переменной?

2. Что называют корнем уравнения с одной переменной?

3. Приведите пример уравнения, у которого нет корней.

4. Что означает фраза: «Решить линейное уравнение»?

5. Приведите пример линейного уравнения с одной переменной.

6. Как вы думаете, может ли корнем линейного уравнения с одной переменной быть отрицательное число? Если да, то приведите пример.

7. Найдите корень уравнения 2x + 7 = 11.

8. Приведите пример линейного уравнения с одной переменной, имеющего своим корнем число:

а) 0; б) 2; в) -1.

9. Сформулируйте алгоритм решения линейного уравнения ах + b = 0 в случае, когда а ≠ 0.

10. Сформулируйте алгоритм решения линейного уравнения ах + b = сx + d (а ≠ с).

<<< К началу