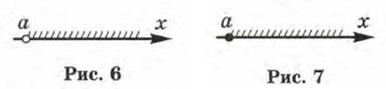§ 5. Координатная прямая

В конце § 3 мы говорили, что нужно уметь свободно переходить от одного вида математической модели к другому, выбирать то, что удобнее. В этой связи весьма полезна известная из курса математики 5—6-го классов такая графическая модель, как координатная прямая.

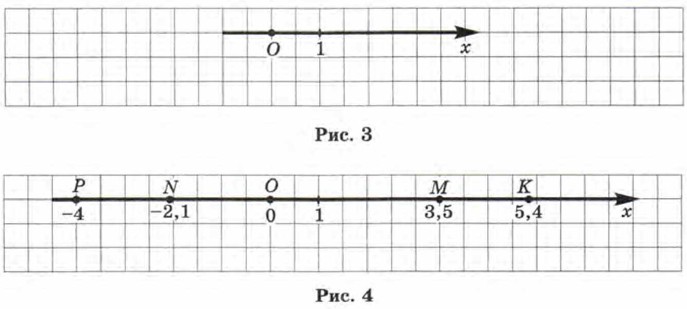
Прямую l, на которой выбрана начальная точка О (начало отсчёта), масштаб (единичный отрезок, т. е. отрезок, длина которого считается равной единице) и положительное направление, называют координатной прямой или координатной осью (рис. 3); употребляют также термин «ось х» («ось у», «ось г» и т. д.).

Каждому числу соответствует единственная точка координатной прямой. Например, числу 3,5 соответствует точка М (рис. 4), которая удалена от начала отсчёта, т. е. от точки О, на расстояние, равное 3,5 (в заданном масштабе), и отложена от точки О в заданном (положительном) направлении. Числу -4 соответствует точка Р (см. рис. 4), которая удалена от точки О на расстояние, равное 4, и отложена от точки О в отрицательном направлении, т. е. в направлении, противоположном заданному.

Можно говорить и о решении обратной задачи. Например, точка К, удалённая от точки О на расстояние 5,4 в положительном (заданном) направлении, соответствует числу 5,4, а точка N, удалённая от точки О на расстояние 2,1 в отрицательном направлении, соответствует числу -2,1 (см. рис. 4).

Указанные числа называют координатами соответствующих точек. Так, на рисунке 4 точка К имеет координату 5,4; точка Р — координату -4; точка М — координату 3,5; точка N — координату -2,1; точка О — координату 0 (нуль). Отсюда и происходит название — «координатная прямая». Образно выражаясь, координатная прямая— это густозаселённый дом, жильцы этого дома — точки, а координаты точек — это номера квартир, в которых живут точки-жильцы.

Зачем нужна координатная прямая? Зачем характеризовать точку числом, а число — точкой? Есть ли в этом какая-либо польза? Да, есть.

Пусть, например, на координатной прямой даны две точки: А — с координатой а и В — с координатой b (обычно в таких случаях пишут короче: А(а), В(b)). Пусть нам надо найти расстояние р между точками А и В. Оказывается, вместо того чтобы делать геометрические измерения, достаточно воспользоваться готовой формулой ρ(А, В) = |а - b| (ρ — «ро» — буква греческого алфавита; впрочем вместо р(А, В) можно писать просто АВ).

Так, на рисунке 4 имеем:

КМ = |5,4 - 3,5| = |1,9| = 1,9;

РМ = |-4 - 3,5| = |-7,5| = 7,5;

PN = |-4 - (-2,1)| = |-4 + 2,1| = |-1,9| = 1,9.

Стремясь к лаконичности рассуждений, математики договорились вместо длинной фразы «точка А координатной прямой, имеющая координату а» использовать короткую фразу «точка а» и на чертеже рассматриваемую точку обозначать её координатой. Так, на рисунке 5 изображена координатная прямая, на которой отмечены точки: -4; -2,1; 0; 1; 3,5; 5,4.

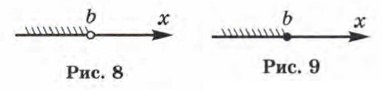
Координатная прямая даёт нам возможность свободно переходить с алгебраического языка на геометрический и обратно. Пусть, например, число а меньше числа b. На алгебраическом языке это записывают так: а < b; на геометрическом языке это означает, что точка а расположена на координатной прямой левее точки b. Впрочем, подчеркнём ещё раз: и алгебраический, и геометрический языки — это разделы одного и того же математического языка, который мы с вами изучаем.

Познакомимся ещё с несколькими элементами математического языка, которые связаны с координатной прямой.

1. Пусть на координатной прямой отмечена точка а. Рассмотрим все точки, которые лежат на прямой правее точки а, и отметим соответствующую часть координатной прямой штриховкой (рис. 6). Это множество точек (чисел) называют открытым лучом и обозначают (а; +∞), где знак +∞ читают так: «плюс бесконечность»; оно характеризуется неравенством х > а (под х понимают любую точку луча).

Обратите внимание: точка а открытому лучу не принадлежит. Если же эту точку надо присоединить к открытому лучу, то пишут х > а или [а; +∞) (перед а ставят не круглую, а квадратную скобку), а на чертеже такую точку обозначают не светлым, как на рисунке 6, а закрашенным кружком (рис. 7). Если про множество точек (а; +∞) говорят, что это — открытый луч, то для множества точек [а; +∞) употребляют термин луч (без прилагательного «открытый»).

2. Пусть на координатной прямой отмечена точка b. Рассмотрим все точки, которые лежат на прямой левее точки b, и отметим соответствующую часть координатной прямой штриховкой (рис. 8). Это множество точек (чисел) также называют открытым лучом и обозначают (-∞; b), где знак —читается: «минус бесконечность». Оно характеризуется неравенством х < b.

Снова обращаем ваше внимание на то, что точка b открытому лучу не принадлежит. Если же мы эту точку хотим присоединить к открытому лучу, то будем писать х ≤ b или (-∞; b] и на чертеже точку b закрашивать (рис. 9); для (-∞; b] также будем употреблять термин луч.

Окончание >>>