§ 6. Координатная плоскость

На координатной прямой «прописаны» точки-жильцы, у каждой точки есть свой номер дома — её координата. Если же точка берётся в плоскости, то для её «прописки» нужно указывать не только номер дома, но и номер квартиры. Напомним, как это делается.

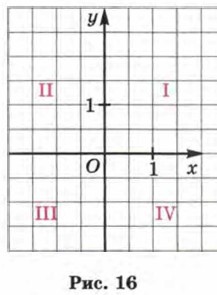
Проведём две взаимно перпендикулярные координатные прямые и будем считать началом отсчёта на обеих прямых точку их пересечения — точку О. Тем самым на плоскости задана прямоугольная система координат (рис. 16), которая превращает обычную плоскость в координатную. Точку О называют началом координат, координатные прямые (ось х и ось у) называют осями координат, а прямые углы, образованные осями координат, называют координатными углами. Координатные углы нумеруют так, как показано на рисунке 16.

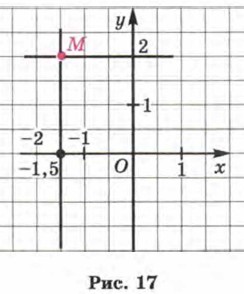
А теперь обратимся к рисунку 17, где изображена прямоугольная система координат и отмечена точка М. Проведём через точку М прямую, параллельную оси у. Прямая пересекает ось х в некоторой точке, у этой точки есть координата на оси х (для точки, изображённой на рисунке 17, эта координата равна —1,5), её называют абсциссой точки М. Далее проведём через точку М прямую, параллельную оси х. Прямая пересекает ось у в некоторой точке, у этой точки есть координата на оси у (для точки М, изображённой на рисунке 17, эта координата равна 2), её называют ординатой точки М. Коротко пишут так: М(х; у) (для точки на рисунке 17 имеем М(-1,5; 2)). Абсциссу записывают на первом месте, ординату — на втором.

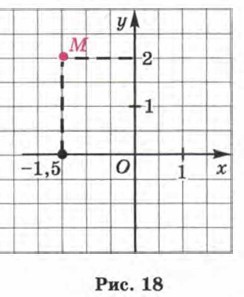
Используют, если в этом есть необходимость, и другую форму записи: х = -1,5; у = 2.

Замечание 1. На практике для отыскания координат точки М обычно вместо прямых, параллельных осям координат и проходящих через точку М, строят отрезки этих прямых от точки М до осей координат (рис. 18).

Замечание 2. В предыдущем параграфе мы ввели разные обозначения для числовых промежутков. В частности, как мы условились, запись (3; 5) означает, что на координатной прямой рассматривается интервал с концами в точках 3 и 5. В настоящем же параграфе пару чисел мы рассматриваем как координаты точки; например, (3; 5) — это точка на координатной плоскости с абсциссой 3 и ординатой 5. Как же правильно по символической записи определить, о чём идёт речь: об интервале или о координатах точки? Обычно это бывает ясно из контекста.

Учитывая введённые термины и обозначения, горизонтальную координатную прямую называют осью абсцисс или осью х, а вертикальную координатную прямую — осью ординат или осью у. Обозначения х, у используют обычно при задании на плоскости прямоугольной системы координат (см. рис. 16) и часто говорят так: дана система координат хОу. Впрочем, встречаются и другие обозначения, например, на рисунке 19 (на с. 36) задана система координат tOs.

Алгоритм отыскания координат точки М, заданной в системе координат хОу
1. Провести через точку М прямую, параллельную оси у, и найти координату точки пересечения этой прямой с осью х — это будет абсцисса точки М.
2. Провести через точку М прямую, параллельную оси х, и найти координату точки пересечения этой прямой с осью у — это будет ордината точки М.

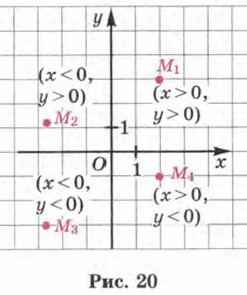
Именно так мы и действовали, находя координаты точки М на рисунке 17.

Если точка М₁(х; у) принадлежит первому координатному углу, то х > 0, у > 0; если точка М₂(х; у) принадлежит второму координатному углу, то х < 0, у > 0; если точка М₃(х; у) принадлежит третьему координатному углу, то х < 0, у < 0; если точка М₄(х; у) принадлежит четвёртому координатному углу, то х > 0, у < 0 (рис. 20).

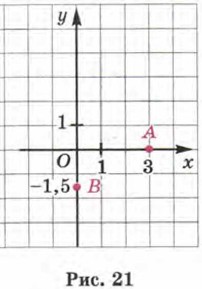
А что будет, если точка, координаты которой надо найти, лежит на одной из осей координат? Пусть точка А лежит на оси х, а точка В — на оси у (рис. 21). Проводить через точку А прямую, параллельную оси у, и находить точку пересечения этой прямой с осью х не имеет смысла, поскольку такая точка пересечения уже есть — это точка А, её координата (абсцисса) равна 3. Точно так же не нужно проводить через точку А прямую, параллельную оси x: сама ось х пересекает ось у в точке О с координатой (ординатой) 0. В итоге для точки А получаем А(3; 0). Аналогично для точки В получаем В(0; -1,5). А для точки О имеем 0(0; 0).

Вообще любая точка на оси х имеет координаты (х; 0), а любая точка на оси у — координаты (0; у).

Окончание >>>