§ 7. Линейное уравнение с двумя переменными и его график (продолжение)

Вообще справедлива следующая теорема.

Теорема 1.

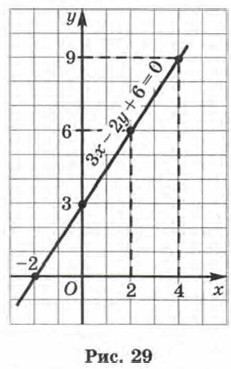
Если хотя бы один из коэффициентов а, b линейного уравнения ах + by + с = 0 отличен от нуля, то графиком уравнения служит прямая линия.

Пример 2. Построить график уравнения 3x - 2у + 6 = 0.

Р е ш е н и е. Подберём несколько решений заданного уравнения:

1) (0; 3); в самом деле, если х = 0, у = 3, то 3 • 0 - 2 • 3 + 6 = 0 — верное равенство (в уравнение 3x - 2у + 6 = 0 мы подставили значения х = 0, у = 3);

2) (-2; 0); действительно, если х = -2, у = 0, то 3 • (-2) - 2 • 0 + 6 = 0 — верное равенство;

3) (2; 6); если x = 2, y = 6, то 3 • 2 - 2 • 6 + 6 = 0 — верное равенство;

4) (4; 9); если х = 4, у = 9, то 3 • 4 - 2 • 9 + 6 = 0 — верное равенство.

Построим точки (0; 3), (-2; 0), (2; 6), (4; 9) на координатной плоскости хОу. Они лежат на одной прямой, проведём её (рис. 29). Эта прямая и есть график уравнения 3х - 2у + 6 = 0.

Пример 2 решён верно, но, признаемся, очень нерационально. Почему? Давайте рассуждать.

1. Мы знаем, что графиком линейного уравнения 3х - 2у + 6 = 0 является прямая (это утверждается в теореме 1). Чтобы провести прямую, достаточно указать две её точки. Через две точки можно провести прямую и притом только одну — этому нас учит геометрия. Поэтому построенные выше четыре точки— это явный перебор. Достаточно было построить точки (0; 3) и (-2; 0) и с помощью линейки провести через них прямую.

2. Решения данного уравнения мы подбирали, т. е. угадывали. Угадать что-либо всегда труднее, чем действовать по определённому правилу. Нельзя ли было и здесь не угадывать, а действовать по какому-то правилу? Можно. Например, так. Дадим переменной х конкретное значение, например х = 0 (обычно пишут x₁ = 0). Подставив это значение в уравнение 3x - 2у + + 6 = 0, получим 3 • 0 - 2у + 6 = 0, т.е. -2у + 6 = 0. Из этого уравнения находим у = 3 (обычно пишут у₁ = 3). Значит, если х = 0, то у = 3; пара (0; 3) — решение данного уравнения.

Дадим переменной х ещё одно конкретное значение, например х = -2 (обычно пишут х₂ = -2). Подставив это значение в уравнение 3x - 2у + 6 = 0, получим 3 • (-2) - 2у + 6 = 0, т. е. -2у = 0. Из этого уравнения находим у = 0 (обычно пишут у₂ = 0). Значит, если х = -2, то у = 0; пара (-2; 0) — решение данного уравнения.

Вот теперь мы в состоянии сформулировать алгоритм построения графика линейного уравнения ах + by + с = 0 (где, напомним, а, b, с — любые числа, но a ≠ 0, b ≠ 0).

Алгоритм построения графика уравнения ах + by + с = 0, где а ≠ 0, b ≠ 0

1. Придать переменной х конкретное значение х = х₁; найти из уравнения ах₁ + by + с — 0 соответствующее значение у = у₁.
2. Придать переменной х другое значение х = х₂; найти из уравнения ах₂ + by + с = 0 соответствующее значение у =y₂.
3. Построить на координатной плоскости хОу точки (x₁; y₁) и (x₂; у2).
4. Провести через эти две точки прямую — она и будет графиком уравнения ах + by + с = 0.

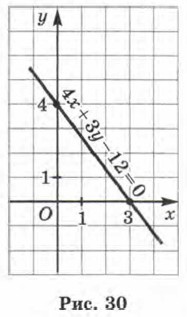
Замечание. Чаще всего на первом шаге алгоритма берут значение х = 0. Второй шаг иногда немного изменяют: полагают у = 0 и находят соответствующее значение х.

Пример 3. Построить график уравнения

4х + 3у - 12 = 0.

Р е ш е н и е. Будем действовать по алгоритму (с учётом замечания).

1) Положим х = 0, подставим это значение в уравнение 4х + 3у - 12 = 0, получим 4 • 0 + 3у - 12 = 0, 3у - 12 = 0, у = 4.

2) Положим у = 0, подставим это значение в уравнение 4х + 3у - 12 = 0, получим 4 • х + 3 • 0 - 12 = 0, 4х - 12 = 0, х = 3.

3) Построим на координатной плоскости хОу две точки: (0; 4) — она найдена на первом шаге алгоритма и (3; 0) — она найдена на втором шаге.

4) Проведём через точки (0; 4) и (3; 0) прямую. Это и есть искомый график (рис. 30).

<<< К началу Окончание >>>