|
|
|
|
|
Глава 2. Линейная функция § 8. Линейная функция и её график (продолжение)Вторая ситуация. На складе было 500 т угля. Ежедневно стали увозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней? Здесь математической моделью ситуации является линейная функция у = 500 - 30x. С помощью этой модели нетрудно ответить на вопрос задачи: если х = 2, то у = 440 (в уравнение у = 500 - 30x подставили x = 2 и получили у = 440); если x = 4, то у = 380; если x = 10, то у = 200. Третья ситуация. Турист проехал на автобусе 15 км от пункта А до пункта В, а затем продолжил движение из пункта В в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от пункта А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы? Математической моделью ситуации является линейная функция у = 15 + 4х, где х — время ходьбы (в часах), у — расстояние от А (в километрах). С помощью этой модели отвечаем на вопрос задачи: если x = 2, то у = 23 (в уравнение у = 15 + 4x подставили x = 2 и получили у = 23); если x = 4, то у = 31; если x = 6, то у = 39.
Итак, в каждой из рассмотренных ситуаций математической моделью служит линейная функция. Но (внимание!), строго говоря, все три составленные модели не совсем точны, они не учитывают тех ограничений на переменную, которые вытекают из смысла задачи. Ведь ясно, что в первой ситуации независимая переменная x может принимать только значения 1, 2, 3, ..., поскольку x — число дней. Следовательно, уточнённая математическая модель первой ситуации выглядит так: у = 500 + 30x, где x — натуральное число. Вторую ситуацию необходимо уточнить условием у ≥ 0. Это значит, что независимая переменная x, обозначающая, как и в первой ситуации, число дней, может принимать только значения 1, 2, 3,..., 16. Действительно, если x = 16, то по формуле у = 500 - 30x находим у = 500 - 30 • 16 = 20. Значит, уже на 17-й день вывезти со склада 30 т угля не удастся, поскольку на складе к этому дню останется всего 20 т и процесс вывоза угля придётся прекратить. Следовательно, уточнённая математическая модель второй ситуации выглядит так: у = 500 - 30х, у ≥ 0 или у = 500 - 30х, где х = 1, 2, 3, ..., 16. В третьей ситуации независимая переменная х теоретически может принять любое неотрицательное значение (х = 0, х = 2, х = 3,5 и т.д.), но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нам нужно было принять разумные ограничения для х, скажем, 0 ≤ х ≤ 6 (т. е. турист идёт не более 6 ч). Напомним, что геометрической моделью нестрогого двойного неравенства 0 ≤ х ≤ 6 служит отрезок [0; 6] координатной прямой (рис. 33). Значит, уточнённая модель третьей ситуации выглядит так: у = 15 + 4х, где х принадлежит отрезку [0; 6].
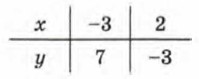
Условимся вместо фразы «х принадлежит множеству X» писать х ∈ Х (читают: «элемент х принадлежит множеству X», ∈ — знак принадлежности). Как видите, наше знакомство с математическим языком постоянно продолжается. Множество натуральных чисел обычно обозначают буквой N. Значит, вместо фразы «х — натуральное число» мы можем использовать соотношение x ∈ N. Если линейную функцию у = kx + m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого числового множества X, то пишут у = kx + m, х ∈ Х. А теперь запишем более точные математические модели для рассмотренных выше трёх ситуаций. Первая ситуация: у = 500 + 30х, х ∈ N. Вторая ситуация: у = 500 - 30х, х ∈ {1, 2, 3, ..., 16}. Третья ситуация: у = 15 + 4х, х ∈ [0; 6]. Пример 2. Построить график линейной функции: а) у = -2х + 1, х ∈ [-3; 2]; б) у = -2х + 1, х ∈ (-3; 2). Р е ш е н и е. а) Составим таблицу для линейной функции y = -2х + 1:
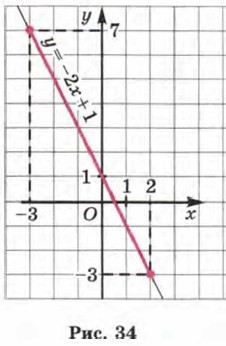
Построим на координатной плоскости хОу точки (-3; 7) и (2; -3) и проведём через них прямую линию. Это график уравнения у = -2х + 1. Далее выделим отрезок, соединяющий построенные точки (рис. 34). Этот отрезок и есть график линейной функции у = -2х + 1, где х е [-3; 2].
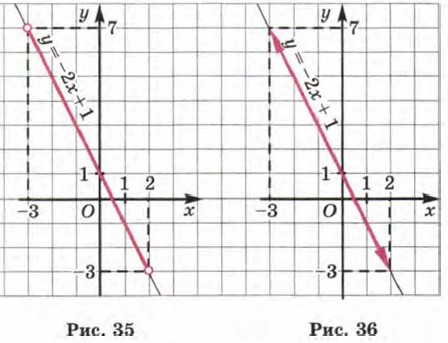
Обычно говорят так: мы построили график линейной функции у = -2х + 1 на отрезке [-3; 2]. б) Чем отличается этот пример от предыдущего? Линейная функция та же (у = -2х + 1), значит, и её графиком служит та же прямая. Но — будьте внимательны! — на этот раз х е (-3; 2), т. е. значения х = -3 и х = 2 не рассматриваются, они не принадлежат интервалу (-3; 2). Как мы отмечали концы интервала на координатной прямой? Светлыми кружочками (рис. 37), об этом мы говорили в § 5. Точно так же и точки (-3; 7) и (2; -3) придётся отметить на чертеже светлыми кружочками.
Это будет напоминать нам о том, что берутся лишь те точки прямой у = -2х + 1, которые лежат между точками, отмеченными кружочками (рис. 35). Впрочем, иногда в таких случаях используют не светлые кружочки, а стрелки (рис. 36). Это непринципиально: главное — понимать, о чём идёт речь.
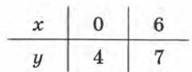
Пример 3. Найти наибольшее и наименьшее значения линейной функции Решение. Составим таблицу для линейной функции
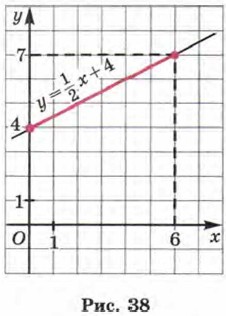
Построим на координатной плоскости хОу точки (0; 4) и (6; 7) и проведём через них прямую — график линейной функции
Нам нужно рассмотреть эту линейную функцию не целиком, а на отрезке [0; 6], т. е. для х е [0; 6]. Соответствующий отрезок графика выделен на чертеже. Замечаем, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 — это и есть наибольшее значение линейной функции Замечаем, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке 38 части прямой, равна 4 — это и есть наименьшее значение линейной функции O т в е т: yнаи6 = 7, унаим = 4.
|
|
|







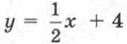 на отрезке [0; 6].
на отрезке [0; 6].