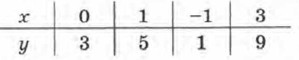|
|
|
|
|
Глава 2. Линейная функция § 8. Линейная функция и её графикАлгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 7, при всей его чёткости и определённости математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у: сначала ах1 + by + с - 0, затем ах2 + by + с = 0? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим. Рассмотрим сначала уравнение 3x - 2у + 6 = 0 (см. пример 2 из § 7), т. е. 2у = 3х + 6. Умножив обе части уравнения на Итак, Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при x = 0 получаем у = 3; при х = -2 имеем у - 0; при х - 2 имеем у = 6; при х = 4 получаем у = 9. Видите, как легко и быстро найдены точки (0; 3), (-2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 7. Точно так же уравнение 5х - 2у = 0 (см. пример 4 из § 7) можно было преобразовать к виду 2у = 5х и, далее, у = 2,5л:; нетрудно найти точки (0; 0) и (2; 5), удовлетворяющие этому уравнению. Наконец, уравнение 3x + 2у - 16 = 0 из того же примера можно было преобразовать к виду 2у = 16 - 3x и, далее, Рассмотрим теперь указанные преобразования в общем виде. Случаи, когда в уравнении ах + by + с = 0 коэффициенты а и b равны нулю, мы рассмотрели в § 7. Там же мы отметили, что в случае, когда а ≠ 0, b = 0, графиком уравнения является прямая, параллельная оси у. Рассмотрим случай, когда b ≠ 0. Имеем
Введя обозначения у = kx + m.
Таким образом, линейное уравнение (1) с двумя переменными х и у в случае, когда b ≠ 0, можно преобразовать к виду у = kx + m, (2) где k, m — числа (коэффициенты). Это частный вид линейного уравнения. Зная, чему равен х, по правилу у = kx + m всегда можно найти, чему равен у. Будем называть уравнение (2) линейной функцией. С помощью уравнения (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например, у = 2х + 3. Тогда если х = 0, то у = 3; если х = 1, то у = 5; если х = -1, то у = 1; если х = 3, то у = 9 и т. д. Обычно эти результаты оформляют в виде таблицы:
Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3 соответственно в точках х = 0,х = 1, х = -1, х = 3. В уравнении (1) переменные х и у равноправны, а в уравнении (2) — нет: конкретные значения мы придаём одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная. Частным случаем теоремы 1 из § 7 является следующая теорема. Теорема 2.
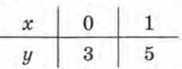
Пример 1. Построить график линейной функции у = 2х + 3. Р е ш е н и е. Составим таблицу:
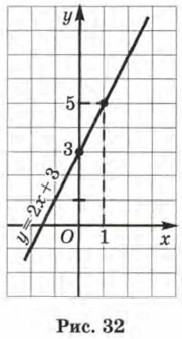
Построим на координатной плоскости хОу точки (0; 3) и (1; 5) и проведём через них прямую. Это и есть график линейной функции у = 2х + 3 (рис. 32). Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции. Приведём примеры. Первая ситуация. На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней? Если пройдёт х дней, то количество у угля на складе (в тоннах) выразится формулой у = 500 + 30х. Таким образом, линейная функция у = 30х + 500 есть математическая модель ситуации. Теперь нетрудно установить, что: при х = 2 имеем у = 560 (в уравнение у = 30х + 500 подставили х = 2 и получили у — 560); при х = 4 имеем у = 620; при х = 10 имеем у = 800.
|
|
|



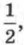 получим
получим 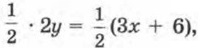 т.е.
т.е. 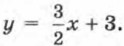 Впрочем, тот же результат мы получили бы, если бы обе части исходного уравнения почленно разделили на 2. Обычно предпочитают в подобных случаях говорить не об умножении, а о почленном делении обеих частей уравнения на одно и то же число.
Впрочем, тот же результат мы получили бы, если бы обе части исходного уравнения почленно разделили на 2. Обычно предпочитают в подобных случаях говорить не об умножении, а о почленном делении обеих частей уравнения на одно и то же число.
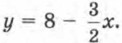 Из этого уравнения можно найти точки (0; 8) и (2; 5), которые ему удовлетворяют.
Из этого уравнения можно найти точки (0; 8) и (2; 5), которые ему удовлетворяют.
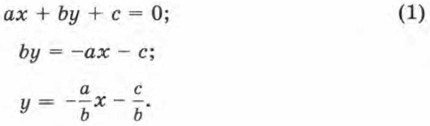
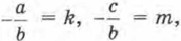 получаем
получаем