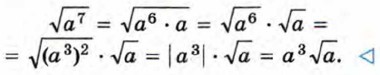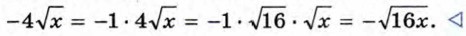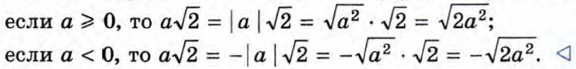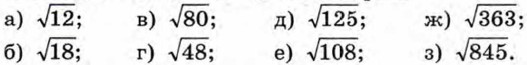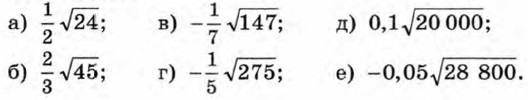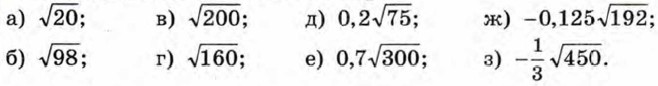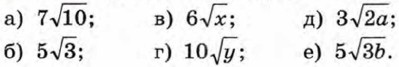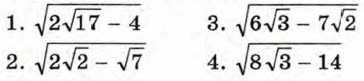|
|
|
|
|
§ 7. Применение свойств арифметического квадратного корня Вынесение множителя за знак корня. Внесение множителя под знак корняСравним значения выражений √50 и 6√2. Чтобы решить эту задачу, преобразуем √50. Представим число 50 в виде произведения 25 • 2 и применим теорему о корне из произведения. Получим
Так как 5√2 < 6√2, то √50 < 6√2. При решении задачи мы заменили √50 произведением чисел 5 и √2. Такое преобразование называют вынесением множителя за знак корня. Значения выражений √50 и 6√2 можно сравнить иначе, представив произведение 6√2 в виде арифметического квадратного корня. Для этого число 6 заменим √36 и выполним умножение корней. Получим 6√2 = √36 • √2 = √72. Так как 50 < 72, то √50 < √72. Значит, √50 < 6√2. При решении задачи вторым способом мы заменили 6√2 выражением √72. Такое преобразование называют внесением множителя под знак корня. Пример 1. Вынесем множитель за знак корня в выражении √a7.
Представим подкоренное выражение а7 в виде произведения а6 • а, в котором множитель а6 является степенью с чётным показателем. Тогда
Пример 2. Внесём множитель под знак корня в выражении -4√x.
Пример 3. Внесём множитель под знак корня в выражении a√2.
Упражнения407. Вынесите множитель за знак корня:
408. Вынесите множитель за знак корня и упростите полученное выражение:
409. Вынесите множитель за знак корня:
410. Внесите множитель под знак корня:
411. Какое из выражений не имеет смысла?
|
|
|



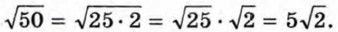
 Выражение √a7 имеет смысл лишь при а ≥ 0, так как если а < 0, то а7 < 0.
Выражение √a7 имеет смысл лишь при а ≥ 0, так как если а < 0, то а7 < 0.