|
|
|
|
|
§ 1. Рациональне дроби и их свойства Основное свойство дроби. Сокращение дробейМы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно равенство Докажем, что это равенство верно не только при натуральных, но и при любых других значениях а, b и с, при которых знаменатель отличен от нуля, т. е. при b ≠ 0 и с ≠ 0.
ас = (bm)с. На основании сочетательного и переместительного свойств умножения имеем: ас = (bс)m. Так как bс ≠ 0, то по определению частного
Значит,
Мы показали, что для любых числовых значений переменных а, b и с, где b ≠ 0 и с ≠ 0, верно равенство
Равенство (1) сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причём b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю. Равенство (1) выражает основное свойство рациональной дроби:
Например,
Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.
Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведём примеры. Пример 1. Приведём дробь
Множитель 5у2 называют дополнительным множителем к числителю и знаменателю дроби Пример 2. Приведём дробь
Дробь
Пример 3. Сократим дробь
Сократим полученную дробь на общий множитель а + 3:
Итак,
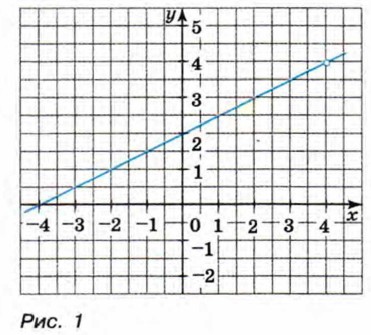
Пример 4. Построим график
Графиком функции
|
|
|



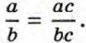
 Пусть
Пусть 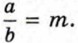 Тогда по определению частного а = bm. Умножим обе части этого равенства на с:
Тогда по определению частного а = bm. Умножим обе части этого равенства на с:
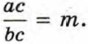
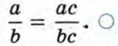

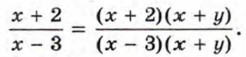
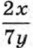 к знаменателю 35у3.
к знаменателю 35у3.
 Так как 35у3 = 7у • 5у2, то, умножив числитель и знаменатель дроби
Так как 35у3 = 7у • 5у2, то, умножив числитель и знаменатель дроби 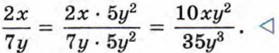
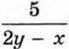 к знаменателю х - 2у.
к знаменателю х - 2у.
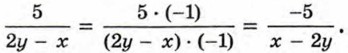
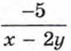 можно заменить тождественно равным выражением
можно заменить тождественно равным выражением 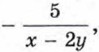 поставив знак «минус» перед дробью и изменив знак в числителе:
поставив знак «минус» перед дробью и изменив знак в числителе: 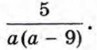
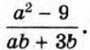
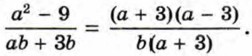
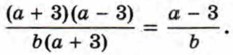
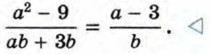
 функции
функции
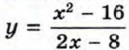 -- множество всех чисел, кроме числа 4. Сократим дробь
-- множество всех чисел, кроме числа 4. Сократим дробь 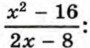
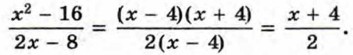
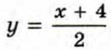 является прямая, а графиком функции
является прямая, а графиком функции 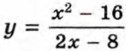 -- та же прямая, но с «выколотой» точкой (4; 4) (рис. 1).
-- та же прямая, но с «выколотой» точкой (4; 4) (рис. 1).