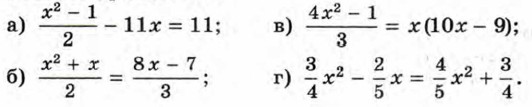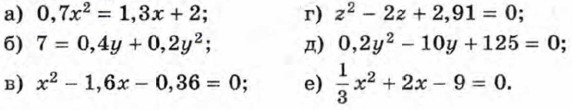|
§ 8. Квадратное уравнение и его корни



Формула корней квадратного уравнения (окончание)
Упражнения
533. Вычислите дискриминант квадратного уравнения и укажите число его корней:
|
а) 2x2 + 3х + 1 = 0;
б) 2х2 + х + 2 = 0;
|
в) 9x2 + 6х + 1 = 0;
г) х2 + 5х - 6 = 0.
|
534. Решите уравнение:
|
а) 3x2 - 7х + 4 = 0;
б) 5x2 - 8л: + 3 = 0;
в) 3x2 - 13x + 14= 0;
г) 2у2 - 9y + 10 = 0;
|
д) 5у2 - 6у + 1 = 0;
е) 4х2 + x - 33 = 0;
ж) у2 - 10у - 24 = 0;
з) р2 + р - 90 = 0.
|
535. Решите уравнение:
|
а) 14x2 - 5х — 1 = 0;
б) -у2 + 3у + 5 = 0;
в) 2х2 + x + 67 = 0;
|
г) 1- 18р + 81р2 = 0;
д) -11у + у2 - 152 = 0;
е) 18 + 3x2 - х = 0.
|
536. Найдите корни уравнения:
|
а) 5x2 - 11x + 2 = 0;
б) 2р2 + 7р - 30 = 0;
в) 9у2 - 30у + 25 = 0;
|
г) 35x2 + 2х - 1 = 0;
д) 2у2 - у - 5 = 0;
е) 16x2 - 8x + 1 = 0.
|
537. При каких значениях х:
а) трёхчлен х2 - 11х + 31 принимает значение, равное 1;
б) значения многочленов х2 - 5 - 3 и 2х - 5 равны;
в) двучлен 7x + 1 равен трёхчлену 3х2 - 2х + 1;
г) трёхчлен -2x2 + 5х + 6 равен двучлену 4х2 + 5х?
538. При каких значениях х принимают равные значения:
539. Решите уравнение, используя формулу (II):
|
а) 3x2 - 14x + 16 = 0;
б) 5х2 - 16x + 3 = 0;
в) х2 + 2х - 80 = 0;
г) х2 - 22x - 23 = 0;
|
д) 4x2 - 36x + 77 = 0;
е) 15у2 - 22у — 37 = 0;
ж) 7z2 - 20z + 14 = 0;
з) у2 -10у - 25 = 0.
|
540. Решите уравнение:
|
а) 8x2 - 14x + 5 = 0;
б) 12х2 + 16х - 3 = 0;
в) 4x2 + А4х + 1 = 0;
г) х2 - 8х - 84 = 0;
|
д) х2 + 6х - 19 = 0;
е) 5х2 + 26х - 24 = 0;
ж) х2 - 34х + 289 = 0;
з) 3х2 + 32х + 80 = 0.
|
541. Решите уравнение:
|
а) 2х2 - 5х - 3 = 0;
б) 3х2 - 8х + 5 = 0;
в) 5х2 + 9х + 4 = 0;
г) 36у2 - 12у + 1 = 0;
|
д) 3t2 - 3t + 1 = 0;
е) х2 + 9х - 22 = 0;
ж) у2 - 12у + 32 = 0;
з) 100x2 - 160x + 63 = 0.
|
542. Решите уравнение:
|
а) 5x2 = 9х + 2;
б) -х2 = 5х - 14;
в) 6x + 9 = х2;
г) z - 5 = z2 - 25;
|
д) у2 = 52у - 576;
е) 15y2 - 30 = 22у + 7;
ж) 25р2 = 10р - 1;
з) 299x2 + 100x = 500 - 101x2.
|
543. Решите уравнение:
|
а) 25 = 26x - x2;
б) 3х2 = 10 - 29x;
в) у2 = 4у + 96;
|
г) 3р2 + 3 = 10р;
д) x2 - 20x = 20х + 100;
е) 25x2 - 13x = 10x2 - 7.
|
544. Найдите корни уравнения:
545. Решите уравнение:
|
а) (x + 4)2 = 3x + 40;
б) (2x - 3)2 = 11x - 19;
в) 3(х + 4)2 = 10x + 32;
г) 15x2 + 17 = 15(х + 1)2;
|
д) (x + 1 )2 = 7918 -2х;
е) (х + 2)2 = 3131 - 2x;
ж) (х + 1)2 = (2х - 1)2;
з) (x - 2)2 + 48 = (2 - 3x)2.
|
546. Решите уравнение:
547. Найдите корни уравнения и укажите их приближённые значения в виде десятичных дробей с точностью до 0,01:
|
а) 5х2 - х - 1 = 0;
б) 2х2 + 7х + 4 = 0;
|
в) 3(у2 - 2) - у = 0;
г) у2 + 8(y - 1) = 3.
|
548. Решите уравнение х2 = 0,5х + 3 сначала графически, а затем с помощью формулы корней.
549. (Для работы в парах.) Решите графически уравнение:
а) x2 - 2х - 1 = 0; б) x2 - 4х + 2 = 0.
1) Обсудите друг с другом, в каком виде удобно представить уравнение.
2) Распределите, кто выполняет задание а), а кто — задание б), и выполните их.
3) Найдите корни каждого из уравнений с помощью формулы корней квадратного уравнения и сравните их со значениями, найденными при графическом решении.
550. Найдите корни уравнения и укажите их приближённые значения в виде десятичных дробей с точностью до 0,01 (воспользуйтесь калькулятором):
551. Решите уравнение:
<<< К началу Ответы >>>
|